
已知函数 的图象经过坐标原点,且
的图象经过坐标原点,且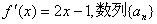 的前
的前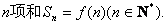
(I)求数列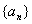 的通项公式;
的通项公式;
(II)若数列 满足
满足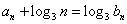 ,求数列
,求数列 的前n项和。
的前n项和。
(Ⅲ)设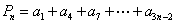 ,
,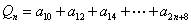 ,其中
,其中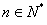 ,试比较
,试比较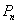 与
与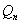 的大小,并证明你的结论。
的大小,并证明你的结论。
思路点拨:本题将数列与函数、导数知识有机的结合在一起,综合考查了导数的逆用,对数的运算、等差数列、等差数列的求和、错位相减法等知识点以及分析问题、综合解决问题的能力。(Ⅰ)首先利用导数知识求出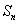 的关系式,然后利用
的关系式,然后利用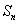 与
与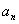 的关系求
的关系求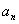 ;(Ⅱ)利用对数知识求出
;(Ⅱ)利用对数知识求出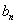 ,然后利用错位相减法求数列
,然后利用错位相减法求数列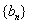 的前n项和,(Ⅲ)是一个是开放性问题,利用等差数列求和公式求出
的前n项和,(Ⅲ)是一个是开放性问题,利用等差数列求和公式求出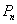 和
和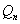 ,然后利用作差法比较大小。
,然后利用作差法比较大小。
解:(I)由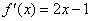 得
得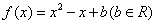
因为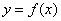 的图象过原点,所以
的图象过原点,所以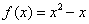
所以 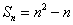 …………2分
…………2分
当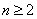 时,
时, 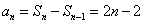
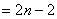
又因为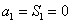 适合
适合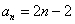
所以数列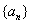 的通项公式为
的通项公式为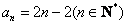 …………4分
…………4分
(II)由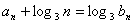 得:
得:
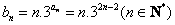 …………5分
…………5分
所以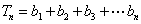
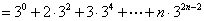 ……(1)
……(1)
所以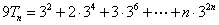 …………(2) -------6分
…………(2) -------6分
(2)-(1)得: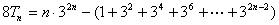
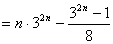
所以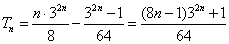 …………8分
…………8分
(Ⅲ)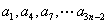 组成以0为首项6为公差的等差数列,所以M
组成以0为首项6为公差的等差数列,所以M 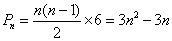 ;
----------------9分
;
----------------9分
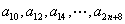 组成以18为首项4为公差的等差数列,所以
组成以18为首项4为公差的等差数列,所以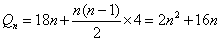 -----------------10分
-----------------10分
故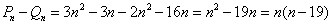 ---------11分
---------11分
所以,对于正整数n,当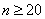 时,
时,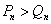 ;
;
当n=19时,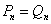 ;
;
当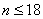 时,
时,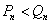 。
------------------------14分
。
------------------------14分
归纳总结:求解有关数列的综合题,首先要善于从宏观上整体把握问题,能透过给定信息的表象,揭示问题的本质,然后在微观上要明确解题方向,化难为易,化繁为简,注意解题的严谨性。数列问题对能力要求较高,特别是运算能力、归纳、猜想能力、转化能力、逻辑推理能力更为突出。而解答题更是考查能力的集中体现,尤其近几年高考加强了数列推理能力的考查,应引起我们足够的重视,因此,在平时要加强对能力的培养.


科目:高中数学 来源:汕头市2009-2010学年度第二学期高三级数学综合测练题(理四) 题型:解答题
已知函数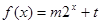 的图象经过点
的图象经过点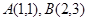 及
及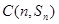 ,
,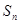 为数列
为数列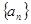
的前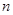 项和.
项和.
(1)求 及
及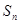 ;
;
(2)若数列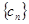 满足
满足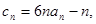 求数列
求数列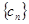 的前项和
的前项和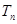 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com