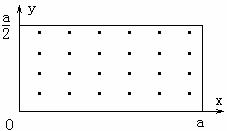
25.(新课标卷)(18分)如图所示，在0≤x≤a、o≤y≤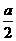范围内有垂直于xy平面向外的匀强磁场，磁感应强度大小为B。坐标原点O处有一个粒子源，在某时刻发射大量质量为m、电荷量为q的带正电粒子，它们的速度大小相同，速度方向均在xy平面内，与y轴正方向的夹角分布在0-90°范围内.己知粒子在磁场中做圆周运动的半径介于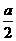到a之间，从发射粒子到粒子全部离开磁场经历的时间恰好为粒子在磁场中做圆周运动周期的四分之一，求最后离开磁场的粒子从粒子源射出时的：

(1)速度大小；

(2)速度方向与y轴正方向夹角正弦。

解析：

设粒子的发射速度为v，粒子做圆周运动的轨道半径为R，由牛顿第二定律和洛伦磁力公式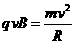，得，解得：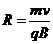

当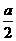＜R＜a时，在磁场中运动时间最长的粒子，其轨迹是圆心为C的圆弧，圆弧与磁场的边界相切，如图所示，设该粒子在磁场中运动的时间为t，依题意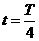，时，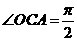

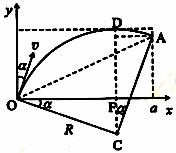
设最后离开磁场的粒子的发射方向与y轴正方向的夹角为α，由几何关系可得：

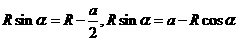再加上，解得：

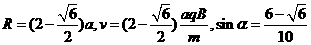
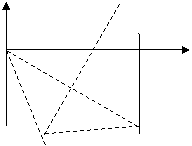
26．(全国卷1)(21分)如下图，在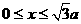区域内存在与xy平面垂直的匀强磁场，磁感应强度的大小为B.在t=0时刻，一位于坐标原点的粒子源在xy平面内发射出大量同种带电粒子，所有粒子的初速度大小相同，方向与y轴正方向的夹角分布在0-180°范围内。已知沿y轴正方向发射的粒子在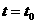时刻刚好从磁场边界上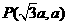点离开磁场。求：

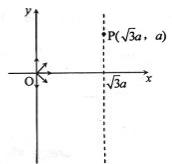
粒子在磁场中做圆周运动的半径R及粒子的比荷q／m；

此时刻仍在磁场中的粒子的初速度方向与y轴正方向夹角的取值范围；

从粒子发射到全部粒子离开磁场所用的时间。

[答案]⑴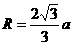　　

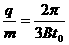
⑵速度与y轴的正方向的夹角范围是60°到120°

⑶从粒子发射到全部离开所用 时间 为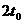

[解析] ⑴粒子沿y轴的正方向进入磁场，从P点经过做OP的垂直平分线与x轴的交点为圆心，根据直角三角形有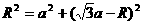

解得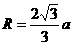

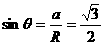，则粒子做圆周运动的的圆心角为120°，周期为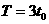

粒子做圆周运动的向心力由洛仑兹力提供，根据牛顿第二定律得

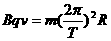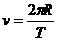，，化简得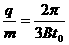

⑵仍在磁场中的粒子其圆心角一定大于120°，这样粒子角度最小时从磁场右边界穿出；角度最大时从磁场左边界穿出。

角度最小时从磁场右边界穿出圆心角120°，所经过圆弧的弦与⑴中相等穿出点如图，根据弦与半径、x轴的夹角都是30°，所以此时速度与y轴的正方向的夹角是60°。

角度最大时从磁场左边界穿出，半径与y轴的的夹角是60°，则此时速度与y轴的正方向的夹角是120°。

所以速度与y轴的正方向的夹角范围是60°到120°

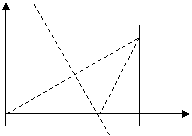
⑶在磁场中运动时间最长的粒子的轨迹应该与磁场的右边界相切，在三角形中两个相等的腰为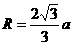，而它的高是

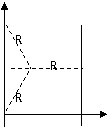
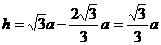，半径与y轴的的夹角是30°，这种粒子的圆心角是240°。所用 时间 为。

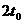所以从粒子发射到全部离开所用 时间 为。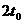

(全国卷2)26(21分)图中左边有一对平行金属板，两板相距为d，电压为V;两板之间有匀强磁场，磁场应强度大小为B0，方向平行于板面并垂直于纸面朝里。图中右边有一边长为a的正三角形区域EFG(EF边与金属板垂直)，在此区域内及其边界上也有匀强磁场，磁感应强度大小为B，方向垂直于纸面朝里。假设一系列电荷量为q的正离子沿平行于金属板面，垂直于磁场的方向射入金属板之间，沿同一方向射出金属板之间的区域，并经EF边中点H射入磁场区域。不计重力

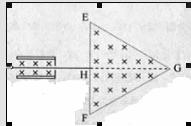
(1)已知这些离子中的离子甲到达磁场边界EG后，从边界EF穿出磁场，求离子甲的质量。

(2)已知这些离子中的离子乙从EG边上的I点(图中未画出)穿出磁场，且GI长为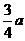，求离子乙的质量。

(3)若这些离子中的最轻离子的质量等于离子甲质量的一半，而离子乙的质量是最大的，问磁场边界上什么区域内可能有离子到达。

解析：

(1)在粒子进入正交的电磁场做匀速直线运动，设粒子的速度为v，电场的场强为E0，根据平衡条件得

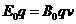　　　　　　　　　　　　　　　 ①

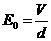　　　　　　　　　　　　　　　　　 ②

由①②化简得

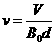　　　　　　　　　　　　　　　　 ③

　　 粒子甲垂直边界EF进入磁场，又垂直边界EF穿出磁场，则轨迹圆心在EF上。粒子运动中经过EG，说明圆轨迹与EG相切，在如图的三角形中半径为

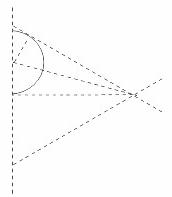
R=acos30°tan15°　　　　　　　　　　　　 ④

tan1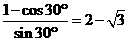5°=　　　　　　　 ⑤

联立④⑤化简得

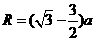　　　　　　　　　　　　　 ⑥

在磁场中粒子所需向心力由洛伦磁力提供，根据牛顿第二定律得

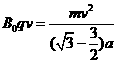　　　　　　　　　　　　　 ⑦

联立③⑦化简得

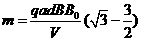　　　　　　　　　　　　 ⑧

(2)由于1点将EG边按1比3等分，根据三角形的性质说明此轨迹的弦与EG垂直，在如图的三角形中，有

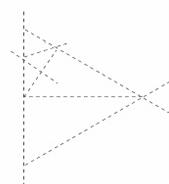
　　　　　 ⑨

同理

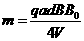　　　　　　　　　　　　 (10)

(3)最轻离子的质量是甲的一半，根据半径公式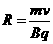离子的轨迹半径与离子质量呈正比，所以质量在甲和最轻离子之间的所有离子都垂直边界EF穿出磁场，甲最远离H的距离为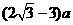，最轻离子最近离H的距离为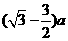，所以在离H的距离为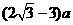到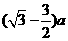之间的EF边界上有离子穿出磁场。

比甲质量大的离子都从EG穿出磁场，期中甲运动中经过EG上的点最近，质量最大的乙穿出磁场的1位置是最远点，所以在EG上穿出磁场的粒子都在这两点之间。

10．一平板车质量m=100 kg，停在水平路面上，车身的平板离地面高h=1.25m，一质量 m=50kg 的小物块置于车的平板上，它到车尾的距离 b=1.00m，与车板间的动摩擦因数μ=0.20，如图3-14所示。 今对平板车施一水平方向的恒力，使车向前行驶，结果物块从车板上滑落。物块刚离开车板的时刻，车向前行驶的距离S0＝2.0m，求物块落地时，落地点到车尾的水平距离s(不计路面与平板车间的摩擦，取g=10m/s2)。(18分)

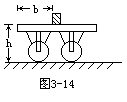
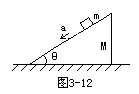
9．如图3-12所示，静止在水平面上的斜劈质量为M、劈角为θ，一质量为m 的物体正沿斜面下滑，下滑的加速度为a(a＜ gsinθ)， 求水平面对斜劈的支持力N和摩擦力f。(13分)

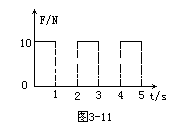
8．质量为 m=5kg的物体，在图3-11 所示的随时间变化的合力F作用下，从静止开始运动。求它前5s的位移。(13分)

7．两个质量相同的小球中间用轻弹簧相连，然后用细绳吊在升降机的顶板上，如图3-5所示。 现升降机正以加速度a匀速上升，若细绳忽然断了， 此时小球1的加速度a1=_______；小球2的加速度a2=________。

6．一物体恰可沿倾角为θ的斜面匀速下滑，若以初速度v0，从斜面下端沿斜面方向抛出此物体，此物体沿斜面前进的最大距离为_____。

5．在环绕地球作匀速圆周运动的航天飞机里　　　　 (　　 )

A．可用弹簧秤称物重　　　　　　 B．可用天平称物体质量

C．可用托利拆利管测舱内气压 　　D．可用测力计测力

4．一个物体在两个共点的恒力作用下，由静止开始运动，若这两个共点力的方向间成锐角。经过一定时间后，突然撤去其中的一个力，则此后物体可能做　　　　　 (　　 )

A．匀加速直线运动　　　　　 B．匀减速直线运动　　　　　　　

C．匀速圆周运动　　　　　　 D．匀变速曲线运动

3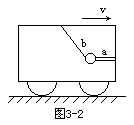．正沿平直轨道向右匀速行驶的车厢内，用水平绳a和倾斜绳b共同固定一个小球，如图3-2所示。若车厢改作加速运动，则两绳的拉力Ta与Tb的变化情况错误的是　(　　 )

A．Ta增大　　　　　 B．Tb减小

C．Tb不变　　　　　 D．Ta、Tb的合力增大