1.

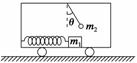
图3－3－10

(2010·日照模拟)在水平地面上运动的小车车厢底部有一质量为m₁的木块，木块和车厢通过一根轻质弹簧相连接，弹簧的劲度系数为k.在车厢的顶部用一根细线悬挂一质量为m₂的小球．某段时间内发现细线与竖直方向的夹角为θ，在这段时间内木块与车厢保持相对静止，如图3－3－10所示．不计木块与车厢底部的摩擦力，则在这段时间内弹簧的形变为(　)　　　　　　　　　　　　　　　

A．伸长量为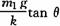　 　　　　 B．压缩量为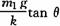

C．伸长量为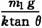　 　　　　　　　　　　 D．压缩量为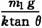

解析：分析m₂的受力情况可得：m₂gtan θ＝m₂a，得出：a＝gtan θ，再对m₁应用牛顿第二定律，得：kx＝m₁a，x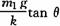＝，因a的方向向左，故弹簧处于伸长状态，故A正确．

答案：A

4.

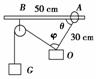
图2－4－13

如图2－4－13所示，在质量为1 kg的重物上系着一条长30 cm的细绳，细绳的另一端连着套在水平棒上可以滑动的圆环，环与棒间的动摩擦因数为0.75，另有一条细绳，其一端跨过定滑轮，定滑轮固定在距离圆环0.5 m的地方．当细绳的端点挂上重物G，而圆环将要滑动时，试问：

(1)长为30 cm的细绳的张力是多少？

(2)圆环将要开始滑动时，重物G的质量是多少？

(3)角φ多大？(环的重力忽略不计)

解析：因为圆环将要开始滑动，所以可以判定本题是在共点力作用下物体的平衡问题．由平衡条件?F_x＝0，?F_y＝0，建立方程有：μF_N－F_Tcos θ＝0，F_N－F_Tsin θ＝0.

所以tan θ＝，θ＝arctan＝arctan.

设想：过O作OA的垂线与杆交于B′点，由AO＝30 cm，tan θ＝得，B′O的长为40 cm.

在直角三角形中，由三角形的边长条件得AB′＝50 cm，但据题设条件AB＝50 cm，故B′点与定滑轮的固定处B点重合，即得φ＝90°.

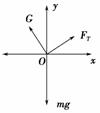
(1)如图所示，选取坐标系，根据平衡条件有：

Gcos θ+F_Tsin θ－mg＝0

F_Tcos θ－Gsin θ＝0.

即　F_T＝8 N.

(2)圆环将要滑动时，得：

m_Gg＝F_Tcot θ，m_G＝0.6 kg.

(3)前已证明φ为直角，故φ＝90°.

答案：(1)8 N　(2)0.6 kg　(3)90°

版权所有：()

版权所有：()

3.

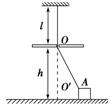
图2－4－12

如图2－4－12所示，一根弹性细绳原长为l，劲度系数为k，将其一端穿过一个光滑小孔O(其在水平地面上的投影点为O′)，系在一个质量为m的滑块A上，A放在水平地面上．小孔O离绳固定端的竖直距离为l，离水平地面高度为h(h<mg/k)，滑块A与水平地面间的最大静摩擦力为正压力的μ倍．问：

(1)当滑块与O′点距离为r时，弹性细绳对滑块A的拉力为多大？

(2)滑块处于怎样的区域内时可以保持静止状态？

解析：(1)当滑块与O′点的距离为r时，弹性细绳的伸长量为Δx＝ .

由胡克定律知，弹性绳的拉力F＝kΔx＝k

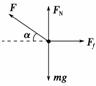
(2)设OA与水平面的夹角为α，分析物体受力如图所示，由平衡条件得：

F_N+Fsin α＝mg

Fcos α＝F_f.

而F＝k，Ff_m＝μF_N

所以有：k·cos α＝F_f≤Ff_m＝μ(mg－Fsin α)＝μ(mg－kh)

其中cos α＝r，故r≤

答案：(1)k

(2)以O′为圆心，以为半径的圆内的任何位置

2.

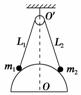
图2－4－11

表面光滑、半径为R的半球固定在水平地面上，球心O的正上方O′处有一无摩擦的定滑轮，轻质细绳两端各系一个小球挂在定滑轮上，如图2－4－11所示，两小球平衡时，若滑轮两侧细绳的长度分别为L₁＝2.4R和L₂＝2.5R，则这两个小球的质量之比m₁∶m₂为(不计球的大小)(　)

A．24∶1　 　　　　　 B．25∶1

C．24∶25　 　　　　 D．25∶24

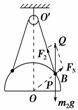
解析：对小球2进行受力分析，如右图所示，显然△O′OP与△PBQ相似．

设OO′＝H，OP＝R，O′P＝L₂，

由相似三角形的性质有m₂g/H＝F_N/R＝F₂/L₂，

则m₂＝F₂H/(gL₂)，同理可得m₁＝F₁H/(gL₁)

而F₁＝F₂，于是m₁/m₂＝L₂/L₁＝25∶24.

答案：D

1.

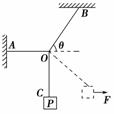
图2－4－10

如图2－4－10所示，用绳OA、OB和OC吊着重物P处于静止状态，其中绳OA水平，绳OB与水平方向成θ角．现用水平向右的力F缓慢地将重物P拉起，用F_A和F_B分别表示绳OA和绳OB的张力，则(　)

A．F_A、F_B、F均增大　 　　　　　　　　　 B．F_A增大，F_B不变，F增大

C．F_A不变，F_B减小，F增大　 　　　　　　 D．F_A增大，F_B减小，F减小

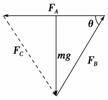
解析：把OA、OB和OC三根绳和重物P看作一个整体，整体受到重力mg，A点的拉力F_A，方向沿着OA绳水平向左，B点的拉力F_B，方向沿着OB绳斜向右上方，水平向右的拉力F而处于平衡状态，有：F_A＝F+F_Bcos θ，F_Bsin θ＝mg，因为θ不变，所以F_B不变．再以O点进行研究，O点受到OA绳的拉力，方向不变，沿着OA绳水平向左，OB绳的拉力，大小和方向都不变，OC绳的拉力，大小和方向都可以变化，O点处于平衡状态，因此这三个力构成一个封闭的矢量三角形(如图)，刚开始F_C由竖直方向逆时针旋转到图中的虚线位置，因此F_A和F_C同时增大，又F_A＝F+F_Bcos θ，F_B不变，所以F增大，所以B正确．

答案：B

12.

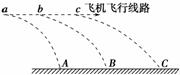
图4－1－30

如图4－1－30所示，在距地面80 m高的水平面上做匀加速直线运动的飞机上每隔1 s依次放下a、b、c三物体，抛出点a、b与b、c间距分别为45 m和55 m，分别落在水平地面上的A、B、C处．求：

(1)飞机飞行的加速度；

(2)刚放下b物体时飞机的速度大小；

(3)b、c两物体落地点BC间距离．

解析：(1)飞机水平方向上，由a经b到c做匀加速直线运动，由Δx＝aT²得，a＝＝＝10 m/s².

(2)因位置b对应a到c过程的中间时刻，故有v_b＝＝50 m/s.

(3)设物体落地时间为t，由h＝gt²得：t＝ ＝4 s，BC间距离为：BC＝bc+v_ct－v_bt，

又v_c－v_b＝aT，得：BC＝bc+aTt＝95 m.

答案：(1)10 m/s²　(2)50 m/s　(3)95 m

版权所有：()

版权所有：()

10.

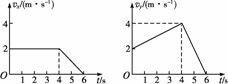
图4－1－28

(2010·西安质检)质量为0.2 kg的物体，其速度在x、y方向的分量v_x、v_y与时间t的关系如图4－1－28所示，已知x、y方向相互垂直，则(　)

A．0-4 s内物体做曲线运动

B．0-6 s内物体一直做曲线运动

C．0-4 s内物体的位移为12 m

D．4-6 s内物体的位移为2 m

答案：AD

9.

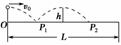
图4－1－27

乒乓球在我国有广泛的群众基础，并有“国球”的美誉，中国乒乓球的水平也处于世界领先地位．现讨论乒乓球发球问题，已知球台长L、网高h，假设乒乓球反弹前后水平分速度不变，竖直分速度大小不变、方向相反，且不考虑乒乓球的旋转和空气阻力．若球在球台边缘O点正上方某高度处以一定的速度被水平发出(如图4－1－27所示)，球恰好在最高点时越过球网，则根据以上信息可以求出(　)

A．发球的初速度大小　 　　　　　　　　B．发球时的高度

C．球从发出到第一次落在球台上的时间　 D．球从发出到对方运动员接住的时间

解析：由运动对称性可知，发球位置距球台的高度等于网高h，发球点到球第一次落在台上P₁点的水平距离为L/4，根据平抛运动的规律h＝gt²，＝v₀t，由此两式可求出发球时的速度v₀和球从发出到第一次落在台上的时间t，所以A、B、C项均正确；但由于不知道对方运动员在何处接住球，故无法求出总时间，D项错误．

答案：ABC

8.

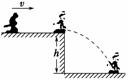
图4－1－26

如图4－1－26所示，高为h＝1.25 m的平台上，覆盖一层薄冰，现有一质量为60 kg的滑雪爱好者，以一定的初速度v向平台边缘滑去，着地时的速度方向与水平地面的夹角为45°(取重力加速度g＝10 m/s²)．由此可知正确的是(　)

A．滑雪者离开平台边缘时的速度大小是5.0 m/s

B．滑雪者着地点到平台边缘的水平距离是2.5 m

C．滑雪者在空中运动的时间为0.5 s

D．滑雪者着地的速度大小为5 m/s

解析：滑雪者平抛运动的时间t＝ ＝0.5 s，落地时的竖直速度v_y＝gt＝5.0 m/s，因着地速度与水平方向的夹角为45°，由vcos 45°＝v₀，vsin 45°＝v_y，可得滑雪者离开平台的水平速度v₀＝5.0 m/s，着地的速度大小为v＝5 m/s，平抛过程的水平距离为x＝v₀t＝2.5 m，故A、B、C、D均正确．

答案：ABCD