1.

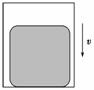
图3－2－10

汶川大地震后，为解决灾区群众的生活问题，党和国家派出大量直升机空投救灾物资．有一直升机悬停在空中向地面投放装有物资的箱子，如图3－2－10所示．设投放初速度为零，箱子所受的空气阻力与箱子下落速度的平方成正比，且运动过程中箱子始终保持图示姿态．在箱子下落过程中，下列说法正确的是(　)

A．箱内物体对箱子底部始终没有压力

B．箱子刚投下时，箱内物体受到的支持力最大

C．箱子接近地面时，箱内物体受到的支持力比刚投下时大

D．若下落距离足够长，箱内物体有可能不受底部支持力而“飘起来”

解析：因为下落速度不断增大，而阻力f∝v²，所以阻力逐渐增大，当f＝mg时，物体开始匀速下落．以箱和物体为整体：(M+m)g－f＝(M+m)a，f增大则加速度a减小．对物体：Mg－F_N＝ma，加速度减小，则支持力F_N增大．所以物体后来受到的支持力比开始时要增大，不可能“飘起来”．

答案：C

5.

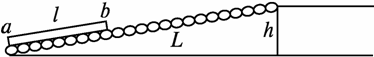
图3－2－9

如图3－2－9所示为某钢铁厂的钢锭传送装置，斜坡长为 L＝20 m，高为h＝2 m，斜坡上紧排着一排滚筒．长为l＝8 m、质量为m＝1×10³ kg的钢锭ab放在滚筒上，钢锭与滚筒间的动摩擦因数为μ＝0.3，工作时由电动机带动所有滚筒顺时针匀速转动，使钢锭沿斜坡向上移动，滚筒边缘的线速度均为v＝4 m/s.假设关闭电动机的瞬时所有滚筒立即停止转动，钢锭对滚筒的总压力近似等于钢锭的重力．取当地的重力加速度g＝10 m/s².试求：

(1)钢锭从坡底(如图3－2－9所示位置)由静止开始运动，直到b端到达坡顶所需的最短时间．

(2)钢锭从坡底(如图3－2－9所示位置)由静止开始运动，直到b端到达坡顶的过程中电动机至少要工作多长时间？

解析：(1)钢锭开始受到的滑动摩擦力为F_f＝μmg＝3×10³ N

由牛顿第二定律有F_f－mgsin α＝ma₁，解得a₁＝2 m/s²

钢锭做匀加速运动的时间t₁＝＝2 s，位移x₁＝a₁t＝4 m

要使b端到达坡顶所需要的时间最短，需要电动机一直工作，钢锭先做匀加速直线运动，当它的速度等于滚筒边缘的线速度后，做匀速直线运动．钢锭做匀速直线运动的位移x₂＝L－l－x₁＝8 m，做匀速直线运动的时间t₂＝＝2 s，所需最短时间t＝t₁+t₂＝4 s.

(2)要使电动机工作的时间最短，钢锭的最后一段运动要关闭电动机，钢锭匀减速上升，b端到达坡顶时速度刚好为零．匀减速上升时F_f+mgsin α＝ma₂，解得a₂＝4 m/s².匀减速运动时间t₃＝＝1 s，匀减速运动位移x₃＝t₃＝2 m，匀速运动的位移x₄＝L－l－x₁－x₃＝6 m，电动机至少要工作的时间t＝t₁+＝3.5 s.

答案：(1)4 s　(2)3.5 s

4．(2010·江苏阜宁中学调研)如图3－2－7所示为学校操场上一质量不计的竖直滑杆，滑杆上端固定，下端悬空，为了研究学生沿杆的下滑情况，在杆的顶部装有一拉力传感器，可显示杆顶端所受拉力的大小，现有一学生(可视为质点)从上端由静止开始滑下，5 s末滑到杆底时速度恰好为零，从学生开始下滑时刻计时，传感器显示拉力随时间变化情况如图3－2－8所示，g取10 m/s²，求：

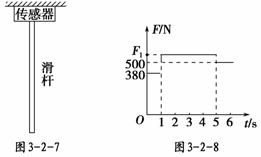
(1)该学生下滑过程中的最大速率；(2)图中力F₁的大小；(3)滑杆的长度．

解析：(1)由于人静止后受拉力F＝500 N，可知，mg＝500 N.

在0-1 s内，人受拉力F＝380 N，人做加速运动，由牛顿第二定律可得：mg－F＝ma₁，

a₁＝2.4 m/s²，v₁＝a₁t₁＝2.4 m/s.

(2)1 s-5 s内人做减速运动，a₂t₂＝a₁t₁，a₂＝0.6 m/s²，

由牛顿第二定律可得：F₁－mg＝ma₂，F₁＝530 N.

(3)L＝a₁t+a₂t＝6 m.

答案：(1)2.4 m/s　(2)530 N　(3)6 m

3．

图3－2－6

在箱式电梯里的台秤秤盘上放着一物体，在电梯运动过程中，某人在不同时刻拍了甲、乙和丙三张照片，如图3－2－6所示，乙图为电梯匀速运动的照片。从这三张照片可判定(　)

A．拍摄甲照片时，电梯一定处于加速下降状态

B．拍摄丙照片时，电梯一定处于减速上升状态

C．拍摄丙照片时，电梯可能处于加速上升状态

D．拍摄甲照片时，电梯可能处于减速下降状态

答案：D

2．2008年9月25日，“神舟七号”载人飞船成功发射，设近地加速时，飞船以5g的加速度匀加速上升，g为重力加速度．则质量为m的宇航员对飞船底部的压力为(　)

A．6mg　 B．5mg　 　　 C．4mg　 　　 D．mg

解析：以人为研究对象，进行受力分析，由牛顿第二定律可知，F－mg＝ma，则F＝m(g+a)＝6mg，再由牛顿第三定律可知，人对飞船底部的压力为6mg.

答案：A

1．在升降电梯内的地面上放一体重计，电梯静止时，晓敏同学站在体重计上，体重计示数为50 kg，电梯运动过程中，某一段时间内晓敏同学发现体重计示数如图3－2－5所示，在这段时间内下列说法中正确的是(　)

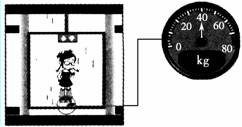
A．晓敏同学所受的重力变小了

B．晓敏对体重计的压力小于体重计对晓敏的支持力

C．电梯一定在竖直向下运动

D．电梯的加速度大小为g/5，方向一定竖直向下

解析：晓敏在这段时间内处于失重状态，是由于晓敏对体重计的压力变小了，而晓敏的重力没有改变，A选项错；晓敏对体重计的压力与体重计对晓敏的支持力是一对作用力与反作用力，大小一定相等，B选项错，以竖直向下为正方向，有：mg－F＝ma，即50g－40g＝50a，解得a＝g/5，方向竖直向下，但速度方向可能是竖直向上，也可能是竖直向下，C选项错，D选项正确．

答案：D

4.

图3－3－12

如图3－3－12所示，在光滑的水平面上放着紧靠在一起的A、B两物体，B的质量是A的2倍，B受到向右的恒力F_B＝2 N，A受到的水平力F_A＝(9－2t) N(t的单位是s)．从t＝0开始计时，则(　)

A．A物体在3 s末时刻的加速度是初始时刻的倍

B．t＞4 s后，B物体做匀加速直线运动

C．t＝4.5 s时，A物体的速度为零

D．t＞4.5 s后，A、B的加速度方向相反

解析：对于A、B整体根据牛顿第二定律有F_A+F_B＝(m_A+m_B)a，开始时合力为11 N,3秒末合力为5 N，故A正确．设A、B间的作用力为F_N，则对B进行分析，由牛顿第二定律可得：F_N+F_B＝m_Ba，解得F_N＝m_B－F_B＝ N．当t＝4 s时，F_N＝0，A、B两物体开始分离，此后B做匀加速直线运动，故B正确；而A做加速度逐渐减小的加速运动，当t＝4.5 s时，A物体的加速度为零而速度不为零，故C错误．t＞4.5 s后，A所受合外力反向，即A、B的加速度方向相反，故D正确．当t＜4 s时，A、B的加速度均为a＝.综上所述，选项A、B、D正确．

答案：ABD

3．如右图所示，车厢里悬挂着两个质量不同的小球，上面的球比下面的球质量大，当车厢向右做匀加速运动时(空气阻力不计)，两个小球稳定后所处的位置下列各图中正确的是(　)

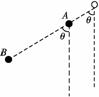
解析：两个小球稳定后与车厢一起向右做匀加速运动，它们的加速度

相同，先使用整体法求得a＝gtan θ，再使用隔离法研究B物体a＝

gtan θ，与竖直方向的角度相同，所以OA与AB在一条线上，B正

确．

答案：B

2.

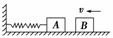
图3－3－11

如图3－3－11所示，在光滑的水平面上，A、B两物体的质量m_A＝2m_B，A物体与轻质弹簧相连，弹簧的另一端固定在竖直墙上，开始时，弹簧处于自由状态，当物体B沿水平向左运动，使弹簧压缩到最短时，A、B两物体间作用力为F，则弹簧给A物体的作用力的大小为(　)

A．F　 　　　　 B．2F　 　　　　 C．3F　 　　　　 D．4F

解析：对B由牛顿第二定律得F＝m_Ba①

对A、B整体由牛顿第二定律得F_弹＝(m_A+m_B)a②

m_A＝2m_B③

由①②③得：F_弹＝3F，所以选项C正确．

答案：C

1.

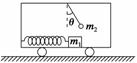
图3－3－10

在水平地面上运动的小车车厢底部有一质量为m₁的木块，木块和车厢通过一根轻质弹簧相连接，弹簧的劲度系数为k.在车厢的顶部用一根细线悬挂一质量为m₂的小球．某段时间内发现细线与竖直方向的夹角为θ，在这段时间内木块与车厢保持相对静止，如图3－3－10所示．不计木块与车厢底部的摩擦力，则在这段时间内弹簧的形变为(　)　

A．伸长量为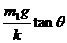　 　　　　 B．压缩量为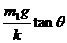

C．伸长量为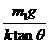　 　　　　　　　　　　 D．压缩量为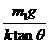

解析：分析m₂的受力情况可得：m₂gtan θ＝m₂a，得出：a＝gtan θ，再对m₁应用牛顿第二定律，得：kx＝m₁a，x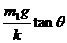＝，因a的方向向左，故弹簧处于伸长状态，故A正确．

答案：A