
题目列表(包括答案和解析)
2. 图像法:
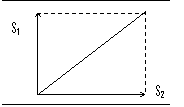
例4:如图所示光滑斜面长度皆为L,高度也相等,两球由静止同时从顶端下滑,若球在图上转折点无能量损失,问那一个小球先到达底端?速度如何?

例5:物体在一条直线运动,先由静止匀加速到3m/s,再匀减速到静止,总共时20秒钟,求20秒物体发生的位移。
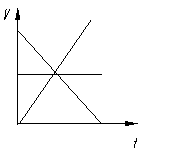
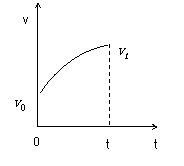 例6:如图14所示,一个做直线运动的物体的速度图象,初速度
例6:如图14所示,一个做直线运动的物体的速度图象,初速度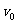 ,末速度
,末速度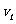 ,在时间
,在时间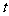 内物体的平均速度
内物体的平均速度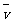 ,则:
,则:
A.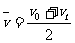 ;
B.
;
B. 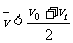 ;
;
 C.
C. 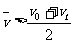 ;
D.
;
D.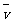 的大小无法确定
的大小无法确定
例6:一质点从A点经B到C作加速直线运动,经图中A、B、C三位置的速度分别为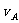 、
、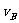 、
、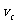 ,且有
,且有 。
。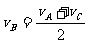 。若质点在AB段加速度恒为
。若质点在AB段加速度恒为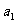 ,BC段加速度恒为
,BC段加速度恒为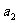 ,则有:
,则有:
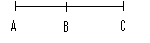 A:
A: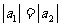 B:
B: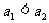
C: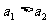 D:不能确定。
D:不能确定。
解:此题借助图像来解非常简单明了。如图所示:
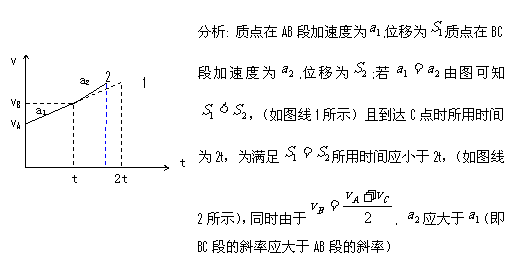
1. 熟练应用公式及推论:
例1:一小车做匀加速直线运动,在某时刻前t1秒内位移为S1,在某时刻后t2秒内位移为S2,求加速度。
例2:某物体匀加速运动,第10秒内位移比第3秒内位移多7米,求加速度。
例3:质点做匀加速直线运动,依次经过如图所示的A、B、C三点,且B点为线段中点。已知质点的AB段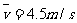 , BC段
, BC段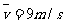 ,那么
,那么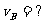
2、速度分解图、位移分解图
速度公式: 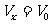
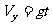
vt的大小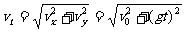
vt的方向可用vt与x轴正方向夹角 来表示,
来表示, 满足下述关系。
满足下述关系。
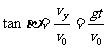
位移公式:
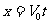
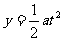
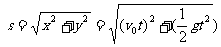
s与x轴正方向的夹角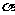 ,
,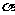 满足下述关系。
满足下述关系。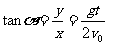
例、从倾角为θ=30°的斜面顶端以初动能E=6J向下坡方向平抛出一个小球,则小球落到斜面上时的动能E /为______J。
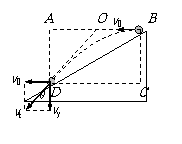 解:以抛出点和落地点连线为对角线画出矩形ABCD,可以证明末速度vt的反向延长线必然交AB于其中点O,由图中可知AD∶AO=2∶
解:以抛出点和落地点连线为对角线画出矩形ABCD,可以证明末速度vt的反向延长线必然交AB于其中点O,由图中可知AD∶AO=2∶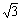 ,由相似形可知vt∶v0=
,由相似形可知vt∶v0=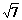 ∶
∶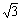 ,因此很容易可以得出结论:E /=14J。
,因此很容易可以得出结论:E /=14J。
本题也能用解析法求解。列出竖直分运动和水平分运动的方程。
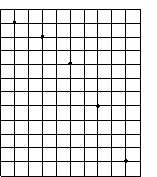 例 已知方格边长a和闪光照相的频闪间隔T,求:v0、g、vc
例 已知方格边长a和闪光照相的频闪间隔T,求:v0、g、vc
解:水平方向: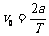 竖直方向:
竖直方向: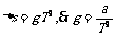
先求C点的水平分速度vx和竖直分速度vy,再求合速度vC:
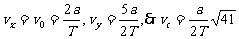
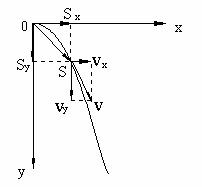 当物体初速度水平且仅受重力作用时的运动,被称为平抛运动。其轨迹为抛物线,性质为匀变速运动。平抛运动可分解为水平方向的匀速运动和竖直方向的自由落体运动这两个分运动。广义地说,当物体所受的合外力恒定且与初速度垂直时,做类平抛运动。
当物体初速度水平且仅受重力作用时的运动,被称为平抛运动。其轨迹为抛物线,性质为匀变速运动。平抛运动可分解为水平方向的匀速运动和竖直方向的自由落体运动这两个分运动。广义地说,当物体所受的合外力恒定且与初速度垂直时,做类平抛运动。
1、分运动:
水平方向:匀速直线运动;
竖直方向:自由落体运动。
3.分运动的性质决定合运动的性质及合运动的轨迹。
① 分运动是匀速直线运动合运动必是匀速直线运动;
② 分运动互成角度,若一个是匀速直线运动,一个是匀变速运动,合运动必是匀变速运动,轨迹必为曲线运动。
③ 分运动互成角度,两个都是初速度为零的匀加速直线运动,其合运动必为初速度为零的匀变速直线运动。
④ 分运动互成角度,一个是初速度为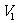 加速度为
加速度为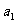 匀变速直线运动;一个是初速度为
匀变速直线运动;一个是初速度为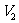 加速度为
加速度为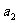 匀变速直线运动;其合运动可能是匀变速直线运动,也可能是匀变速曲线运动。
匀变速直线运动;其合运动可能是匀变速直线运动,也可能是匀变速曲线运动。
⑤ 合运动与分运动具有等时性:
例: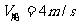 ;
;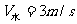 ;
;
求(1)船过河的最短时间;(2)若过河时使船航行的路程最短,那么需要多少时间?(3)如要使船在对岸登陆,且登陆点距出发点沿河岸距离为560米,求船在静水中的最小速度?
2. 凡是矢量一律可用平行四边形法则;

1. 力的独立作用性原理:
|
|||||
 |
|||||
|
|||||
2. 竖直上抛
一般定 为正方向,则
为正方向,则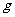 为负值
为负值
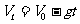
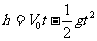
① 物体上升最高点所用时间: 
② 上升的最大高度: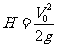
③ 物体下落时间(从抛出点--回到抛出点):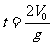
④落地速度: 
结论:上升过程中(某一位置速度)和下落过程中通过某一位置的
速度大小总是相等,方向相反。
1. 自由落体: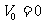 加速度为
加速度为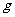 的匀加速直线运动
的匀加速直线运动
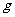 的取值与那些因素有关 ①与纬度有关g赤〈g两极
的取值与那些因素有关 ①与纬度有关g赤〈g两极
②与高度有关
③与地下矿藏有关
自由落体公式
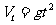
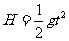
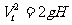
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com