
题目列表(包括答案和解析)
21.(本小题共14分)
在平面直角坐标系xoy上,给定抛物线L:y=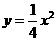 。实数p,q满足
。实数p,q满足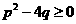 ,x1,x2是方程
,x1,x2是方程
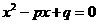 的两根,记
的两根,记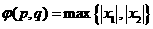 。
。
(1)过点,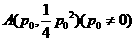 ,(p0≠ 0)作L的切线教y轴于点B。证明:对线段AB上任一点Q(p,q)有
,(p0≠ 0)作L的切线教y轴于点B。证明:对线段AB上任一点Q(p,q)有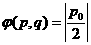 ;
;
(2)设M(a,b)是定点,其中a,b满足a2-4b>0,a≠ 0。过设M(a,b)作L的两条切线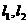 ,切点分别为
,切点分别为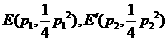 ,
,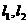 与y轴分别交与F,。线段EF上异于两端点的点集记为X。证明:M(a,b)
与y轴分别交与F,。线段EF上异于两端点的点集记为X。证明:M(a,b) 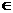 X
X
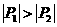

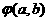
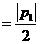
(3)设D={
(x,y)|y≤x-1,y≥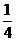 (x+1)2-
(x+1)2-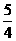 }。当点(p,q)取遍D时,求
}。当点(p,q)取遍D时,求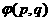 的最小值
(记为
的最小值
(记为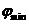 )和最大值(记为
)和最大值(记为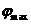 )
)
20.(本小题共14分)
设b>0,数列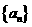 满足a1=b,
满足a1=b,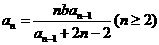 。
。
(1)求数列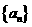 的通项公式;
的通项公式;
(2)证明:对于一切正整数n,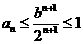
19.(本小题满分14分)
设圆C与两圆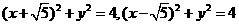 中的一个内切,另一个外切。
中的一个内切,另一个外切。
(1)求圆C的圆心轨迹L的方程
(2)已知点M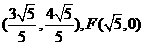 ,且P为L上动点,求
,且P为L上动点,求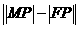 的最大值及此时P的坐标.
的最大值及此时P的坐标.
18.(本小题满分13分)
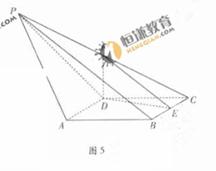 在椎体P-ABCD中,ABCD是边长为1的棱形,且∠DAB=60
在椎体P-ABCD中,ABCD是边长为1的棱形,且∠DAB=60 ,
,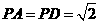 ,PB=2, E,F分别是BC,PC的中点
,PB=2, E,F分别是BC,PC的中点
(1)证明:AD 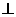 平面DEF
平面DEF
(2) 求二面角P-AD-B的余弦值
17.为了解甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽出取14件和5件,测量产品中的微量元素x,y的含量(单位:毫克)。下表是乙厂的5件产品的测量数据:
|
编号 |
1 |
2 |
3 |
4 |
5 |
|
x |
169 |
178 |
166 |
175 |
180 |
|
y |
75 |
80 |
77 |
70 |
81 |
(1)已知甲厂生产的产品共有98件,求乙厂生产的产品总数。
(2)当产品中的微量元素x,y满足x≥175,y≥75,该产品为优等品。用上述样本数据估计乙厂生产的优等品的数量。
(3)从乙厂抽出的上述5件产品中,随机抽取2件,球抽取的2件产品中的优等品数 的分布列极其均值(即数学期望)。
的分布列极其均值(即数学期望)。
16. (本小题满分12分)
已知函数f(x)=2sin(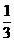 x-
x-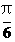 ),x
),x R
R
(1)求f(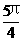 )的值;
)的值;
(2)设α,β [0,
[0,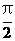 ],f(3α+
],f(3α+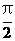 )=
)=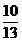 ,f(3β+2π)=
,f(3β+2π)=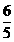 ,求cos(α+β)的值。
,求cos(α+β)的值。
(二)选择题(14---15题,考生只能从中选做一题)
14、(坐标系与参数方程选做题)已知两面线参数方程分别为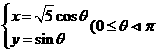 和
和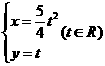 ,它们的交点坐标为___________.
,它们的交点坐标为___________.
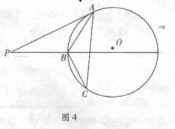
15.(几何证明选讲选做题)如图4,过圆 外一点
外一点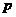 分别作圆的切线和割线交圆于
分别作圆的切线和割线交圆于 ,
,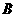
且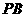 =7,
=7,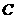 是圆上一点使得
是圆上一点使得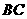 =5,∠
=5,∠ 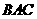 =∠
=∠ 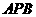 ,
则
,
则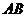 =
。
=
。
9.不等式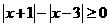 的解是
的解是
10. 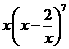 的展开式中,
的展开式中,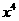 的系数是
(用数字作答)
的系数是
(用数字作答)
11、等差数列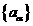 前9项的和等于前4项的和。若
前9项的和等于前4项的和。若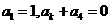 ,则k=____________.
,则k=____________.
12、函数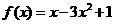 在x=____________处取得极小值。
在x=____________处取得极小值。
13、某数学老师身高176cm,他爷爷、父亲和儿子的身高分别是173cm、170cm和182cm。因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为_____cm.
8.设S是整数集Z的非空子集,如果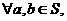 有
有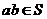 ,则称S关于数的乘法是封闭的,若T,V是Z的两个不相交的非空子集,
,则称S关于数的乘法是封闭的,若T,V是Z的两个不相交的非空子集,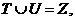 且
且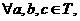 有
有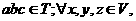 有
有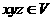 ,则下列结论恒成立的是
,则下列结论恒成立的是
A.
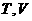 中至少有一个关于乘法是封闭的 B.
中至少有一个关于乘法是封闭的 B. 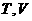 中至多有一个关于乘法是封闭的C.
中至多有一个关于乘法是封闭的C. 中有且只有一个关于乘法是封闭的
D.
中有且只有一个关于乘法是封闭的
D.  中每一个关于乘法都是封闭的
中每一个关于乘法都是封闭的
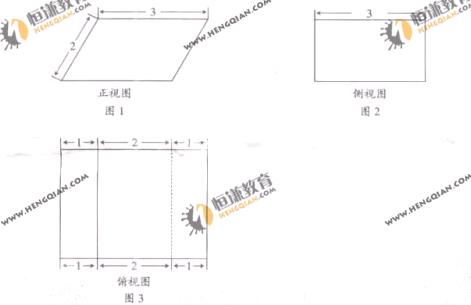
7.如图1-3,某几何体的正视图(主视图)是平行四边形,侧视图(左视图)和俯视图都是矩形,则几何体的体积为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com