
题目列表(包括答案和解析)
26.(10分)已知:如图,⊙O与⊙P相交于A、B两点,点 P在⊙O上,⊙O的弦AC切⊙P于点A,CP及其延长线交⊙P于D、E,过点 E作EF⊥CE交CB的延长线于F。
(1)求证:BC是⊙P的切线;
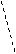
 (2)若CD=2,CB=
(2)若CD=2,CB= ,求EF的长;
,求EF的长;
(3)求以BP、EF为根的一元二次方程;
解:(1)∵点 P在⊙O上。连结PB,
∵CP为直径,∴∠CPB =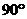 ,
,
∴PB⊥CB,∵B在⊙P上,
∴CB是⊙P的切线。
(2)∵CB是⊙P的切线,∴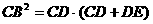 ,∵
,∵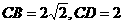 ,
,
∴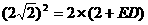 ,∴
,∴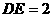 ,∴
,∴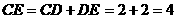 ,
,
∴在⊙P中,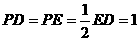 ,
,
在Rt⊿CPB中,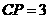 ,
,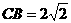 ,∴
,∴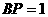 ,
,
∵EF⊥CE,∴∠FEC =∠CBP =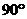 ,∠FCE =∠PCB,∴⊿FCE∽⊿PCB,
,∠FCE =∠PCB,∴⊿FCE∽⊿PCB,
∴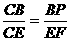 ,而
,而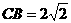 ,
,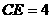 ,
,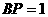 ,∴
,∴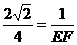 ,∴
,∴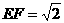
(3)∵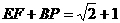 ,
,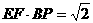
∴所求以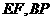 为根的方程是:
为根的方程是: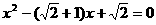
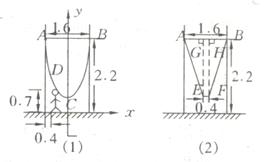
25. (10分)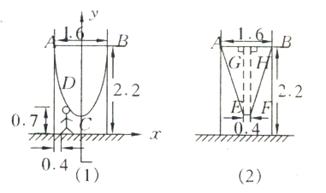 为供孩子们打秋千,把绳子剪断后,中间系上一块长为
为供孩子们打秋千,把绳子剪断后,中间系上一块长为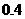 米的木板,除掉系木板用去的绳子后,两边的绳子正好各为2米,木板与地面平行,(1)求绳子未剪断时最低点到地面的距离;(2)求剪断绳子系上木板时,木板到地面的距离。(供选用数据:
米的木板,除掉系木板用去的绳子后,两边的绳子正好各为2米,木板与地面平行,(1)求绳子未剪断时最低点到地面的距离;(2)求剪断绳子系上木板时,木板到地面的距离。(供选用数据: ,
,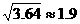 ,
,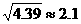 )
)
解:(1)如图,建立直角坐标系,
设二次函数为: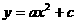
∵D(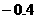 ,
,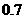 ),
),
B(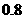 ,
,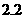 )
)
∴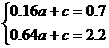
 ∴
∴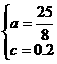 ,∴绳子最低点到地面的距离为
,∴绳子最低点到地面的距离为
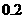 米。
米。
(2)分别作EG⊥AB于G,EH⊥AB于H,
AG =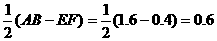
在Rt⊿AGE中,
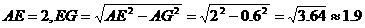
∴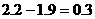 (米)
(米)
∴木板到地面的距离约为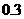 米。
米。
24.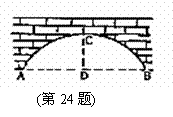 (10分)有一个拱桥是圆弧形,他的跨度为60
(10分)有一个拱桥是圆弧形,他的跨度为60 ,拱高为18
,拱高为18 ,当洪水泛滥跨度小于30
,当洪水泛滥跨度小于30 时,要采取紧急措施。若拱顶离水面只有4
时,要采取紧急措施。若拱顶离水面只有4 时,问是否要采取紧急措施?
解:作出圆弧形的圆心O,
时,问是否要采取紧急措施?
解:作出圆弧形的圆心O,
在Rt⊿OAD中,
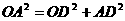 ,而OA =
,而OA = ,AD = 30,CD = 18
,AD = 30,CD = 18
∴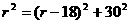
∴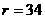
当拱顶里水面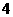 米时,水面所在弦的弦心距为:
米时,水面所在弦的弦心距为:
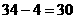 米,设水面所在的弦为
米,设水面所在的弦为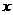 ,由勾股定理可知:
,由勾股定理可知:
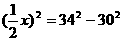 ,∴
,∴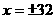 ,负值舍去,∴
,负值舍去,∴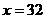
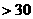
∴不用采取紧急措施。
23.如图:已知一次函数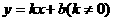 的图象与
的图象与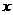 轴、
轴、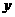 轴分别交于
轴分别交于 、
、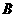 两点,且与反比例函数
两点,且与反比例函数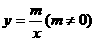 的图象在第一象限交于
的图象在第一象限交于 点,
点,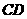 ⊥
⊥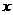 轴,垂足为
轴,垂足为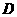 ,
,
若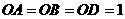 (1)求点
(1)求点 、
、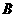 、
、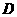 的坐标;(2)求一次函数与反比例函数的解析式;;
的坐标;(2)求一次函数与反比例函数的解析式;;

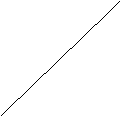
 y
y
C

B
 x
x
A O D
解:(1)∵OA = OB = OD = 1,∴A(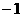 ,0)、B(0,1)、D(1,0);
,0)、B(0,1)、D(1,0);
(2)∵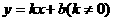 过A、B两点,∴
过A、B两点,∴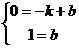
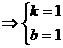
∴所求一次函数为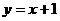 ,
,
∵C(1,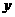 )在
)在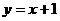 上,∴C(1,2)也在
上,∴C(1,2)也在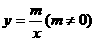 上,∴
上,∴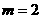 ,
,
∴所求反比例函数为: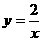 ,
,
22.解:(1)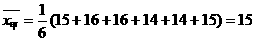 ,
,
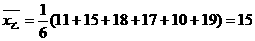
但: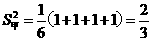 ,
,
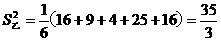 ,
,
∴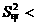
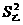 ,
,
∴走甲路更舒适。
(2)设计石阶路的每一级石阶高度为15( ),由于高度一致,平均数一致,所以方差为零,即
),由于高度一致,平均数一致,所以方差为零,即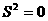 ,这样的石阶路走起来更舒适。
,这样的石阶路走起来更舒适。
21.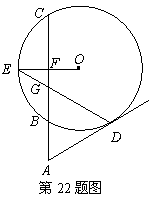 如图,割线ABC与⊙O相交于B、C两点,D为⊙O上一点,E为BC的中点,OE交BC于F,DE交AC于G,∠ADG=∠AGD.
如图,割线ABC与⊙O相交于B、C两点,D为⊙O上一点,E为BC的中点,OE交BC于F,DE交AC于G,∠ADG=∠AGD.
⑴求证:AD是⊙O的切线;
⑵如果AB=2,AD=4,EG=2,求⊙O的半径.
|
∴OE⊥BC于F.
∴∠AGD+∠ODE=∠EGF+∠OED
=90°.……………………2分
连结OD.则OD=OE,
∴∠ODE=∠OED.……………………3分
∵∠AGD=∠ADG,
∴∠ADG+∠ODE=90°,即OD⊥AD.
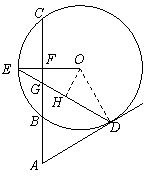 ∴AD是⊙O的切线.……………………5分
∴AD是⊙O的切线.……………………5分
⑵由AD=4,AB=2,AD2=AB·AC,得AC=8.……………………6分
∵AD=AG,∴BG=2,CG=4.
由EG=2,EG·GD=BG·CG,得DG=4.…………………………7分
∴AD=DG=GD,∴∠ADG=60°.
作OH⊥ED于H,则∠EOH=60°.…………………………………8分
在Rt△OEH中,EH=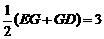 ,……………………………9分
,……………………………9分
∴OE=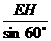 =
=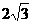 .
.
即⊙O的半径为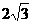 .………………………………………………10分
.………………………………………………10分
20.本题证法多种,要求:1、写出已知,求证、画出图形,2、有完整的证明过程,3、有结论。
19.
解:设平均每年降低成本百分数为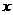 ,根据题意得:
,根据题意得:
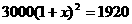
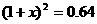
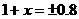
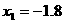 (不符题意,舍去),
(不符题意,舍去),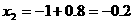
答:平均每年降低成本为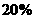 。
。
18.原式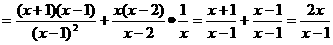
当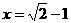 时,原式
时,原式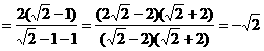
17.原式=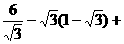
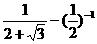
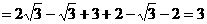
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com