
题目列表(包括答案和解析)
6、随着通讯市场竞争日益激烈,某通讯公司的手机市话收费标准按原标准每分钟降低了a元后,再次下调了25%,现在的收费标准是每分钟b元,则原收费标准每分钟为( )
A、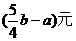 B、
B、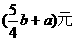 C、
C、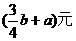 D、
D、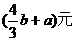
5、用换元法解方程x2+5x+2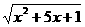 =2时,令
=2时,令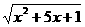 =y,那么原方程变为(
)
=y,那么原方程变为(
)
A、y2+2y+3=0 B、y2+2y-1=0 C、y2+2y-3=0 D、y2+2y+1=0
4、用科学记数法表示2000.4,并保留4个有效数字,正确的是( )
A、2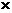 104 B、2.000
104 B、2.000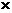 104 C、2.000
104 C、2.000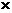 103 D、2.001
103 D、2.001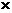 103
103
3、下列计算正确的是( )
A、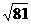 =9 B、(
=9 B、(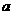 3)2=a9 C、2a2+2a2=4a4 D、
3)2=a9 C、2a2+2a2=4a4 D、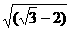 2=
2=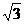 -2
-2
2、函数y=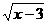 的自变量x的取值范围是( )
的自变量x的取值范围是( )
A、x>3 B、x<3 C、x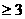 D、x
D、x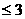
1、计算-1+2=( )
A、-3 B、1 C、-1 D、3
25、 (1) 略 (2) 设AD=x,由已知AD+DE=AB=a得DE=a-x,又AE=m
在Rt△AED中,由勾股定理得: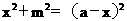
化简整理得: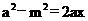 ①
①
在△EBC中,由AE=m,AB=a,得BE=a-m
因为△ADE∽△BEC,所以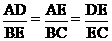 ,
,
即: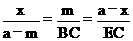 ,
,
解得: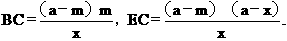
所以△BEC的周长=BE+BC+EC=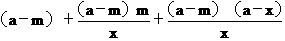
= =
=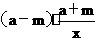
=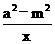 ②
②
把①式代入②,得△BEC的周长=BE+BC+EC=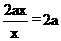 ,
,
所以△BEC的周长与m无关。
24、 解:(1)过点B作BQ⊥OA于点Q.(如图1)
∵ 点A坐标是(-10,0),
∴点A1坐标为(-10+m,-3),OA=10.
 …………………2分
…………………2分
又∵ 点B坐标是(-8,6),
∴BQ=6,OQ=8.
在Rt△OQB中,
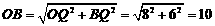 …3分
…3分
∴OA=OB=10,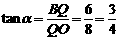 .
.
由翻折的性质可知,PA=OA=10,PB=OB=10, ∴四边形OAPB是菱形,
∴PB∥AO,∴P点坐标为(-18,6), ……………5分
∴P1点坐标为(-18+m,3). ………………6分
(2)①当0<m≤4时,(如图2), 过点B1作B1Q1⊥x轴于点Q1,则B1 Q1=6-3=3,设O1B1 交x轴于点F,∵O1B1∥BO,∴∠α=∠β,
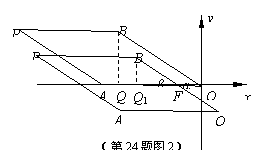 在Rt△FQ1B1中,
在Rt△FQ1B1中,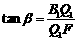 ,
,
∴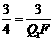 ,∴Q1F=4,
,∴Q1F=4,
∴B1F=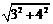 =5,
=5,
∵AQ=OA-OQ=10-8=2,
∴AF=AQ+QQ1+ Q1F=2+m+4=6+m,
∴面积s=3AF =2m+12……9分
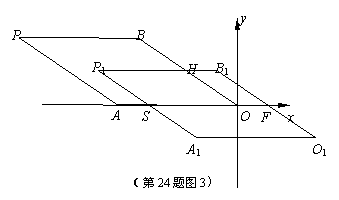
②当4<m<14时,(如图3)
设P1A1交x轴于点S,P1B1交OB
于点H,
由平移性质,得 OH=B1F=5,
此时AS=m-4,
∴OS=OA-AS
=10-(m-4)=14-m,
∴面积s=3OS=3(5+14-m)=-3 m+57. ……12分
23、略
22、解:(1)当CE=4时,四边形ABED是等腰梯形。
理由如下:
在BC上截取CE=AD,连结DE、AE,
∵AD∥BC,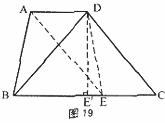
∴四边形AECD是平行四边形。
∴AE=CD=BD。
∵BE=12-4=8>4,即BE>AD,
∴AB不平行于DE,
∴四边形ABED是梯形。
∵AE∥CD,CD=BD,
∴∠AEB=∠C=∠DBC。
在△ABE和△DEB中,
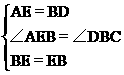
∴△ABE≌△DEB (SAS)。
∴AB=DE,
∴四边形ABED是等腰梯形。
(也可不作辅助线,通过证明△ABD≌EDC而得AB=DE)
(2)当C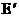 =6时,四边形AB
=6时,四边形AB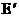 D是直角梯形。
D是直角梯形。
理由如下:
在BC上取一点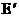 ,使C
,使C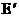 =B
=B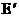 =
=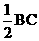 =6,连结D
=6,连结D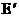 ,
,
∵BD=CD
∴D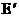 ⊥BC
⊥BC
又∵B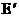 ≠AD,AD∥B
≠AD,AD∥B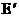 ,
,
∴AB不平行于D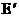
∴四边形AB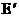 D是直角梯形。
D是直角梯形。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com