
题目列表(包括答案和解析)
1.sin (–270°) = ( )
A.–1 B.0 C.1 D.–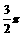
21.(本小题满分13分)
定义:将一个数列中部分项按原来的先后次序排列所成的一个新数列称为原数列的一个子数列.已知无穷等比数列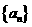 的首项和公比均为
的首项和公比均为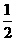 .
.
(1)试求无穷等比子数列 (
( )各项的和;
)各项的和;
(2)已知数列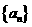 的一个无穷等比子数列各项的和为
的一个无穷等比子数列各项的和为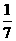 ,求这个子数列的通项公式;
,求这个子数列的通项公式;
(3)证明:在数列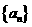 的所有子数列中,不存在两个不同的无穷等比子数列,使得它们各项的和相等.
的所有子数列中,不存在两个不同的无穷等比子数列,使得它们各项的和相等.
解:(1)依条件得: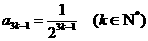 则无穷等比数列
则无穷等比数列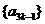 各项的和为:
各项的和为:
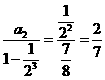 . ……………………………………………………………………3分
. ……………………………………………………………………3分
(2)解法一:设子数列的首项为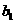 ,公比为
,公比为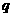 ,由条件得:
,由条件得: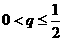 ,
,
则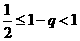 ,即
,即
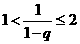 ,
, 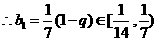 .
.
而  ,则
,则 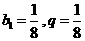 .
.
所以,满足条件的无穷等比子数列存在且唯一,它的首项.公比均为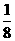 ,
,
其通项公式为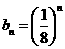 ,
,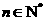 . ………………………………………………7分
. ………………………………………………7分
解法二:由条件,可设此子数列的首项为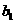 ,公比为
,公比为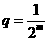
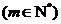 .
.
由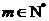
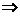
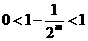
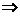
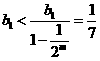 ………… ①
………… ①
又若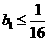 ,则对每一
,则对每一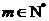 ,都有
,都有
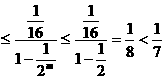 ………… ②
………… ②
从①、②得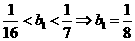 ;则
;则
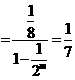
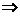
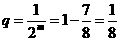 ;
;
因而满足条件的无穷等比子数列存在且唯一,此子数列是首项.公比均为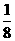 无穷等比子数列,通项公式为
无穷等比子数列,通项公式为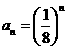 ,
,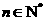 . …………………………………………7分
. …………………………………………7分
(3)假设存在原数列的两个不同的无穷等比子数列,使它们的各项和相等.设这两个
子数列的首项与公比分别为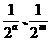 和
和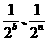 ,其中
,其中 且
且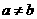 或
或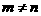 ,则
,则
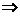
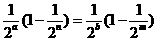 ………… ①
………… ①
若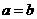 且
且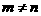 ,则①
,则①
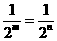

 ,矛盾;若
,矛盾;若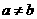 且
且 ,则①
,则①
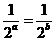

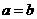 ,矛盾;故必有
,矛盾;故必有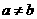 且
且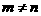 ,不妨设
,不妨设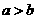 ,则
,则
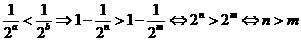 .
.
①
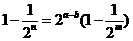

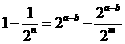 …………
②
…………
②
②
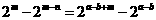

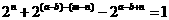
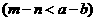 或
或
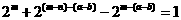
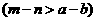 ,两个等式的左,右端的奇偶性均矛盾.
,两个等式的左,右端的奇偶性均矛盾.
故不存在原数列的两个不同的无穷等比子数列,使得它们的各项和相等. ………13分
本资料由《七彩教育网》 提供!
20.(本小题满分13分)
 已知
已知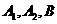 是椭圆
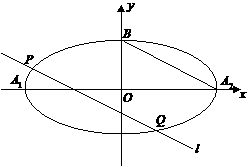
是椭圆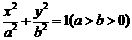 的顶点(如图),直线
的顶点(如图),直线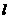 与椭圆交于异于顶点的
与椭圆交于异于顶点的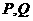 两点,且
两点,且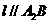 .若椭圆的离心率
.若椭圆的离心率
是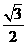 ,且
,且 .
.
(1)求此椭圆的方程;
(2)设直线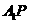 和直线
和直线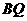 的倾斜角分别
的倾斜角分别
为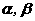 .试判断
.试判断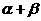 是否为定值?若是,求出此定值;若不是,说明理由.
是否为定值?若是,求出此定值;若不是,说明理由.
解:(1)由已知可得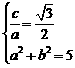 ,所以
,所以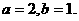 椭圆方程为
椭圆方程为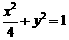 . ……4分
. ……4分
(2)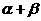 是定值
是定值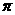 .理由如下:
.理由如下:
由(1),A2(2,0),B(0,1),且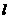 //A2B,所以直线
//A2B,所以直线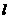 的斜率
的斜率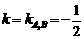 .…6分
.…6分
设直线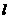 的方程为
的方程为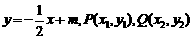 ,
,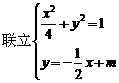 ,
,
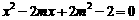

即 ,且
,且
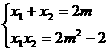 . ………………………9分
. ………………………9分
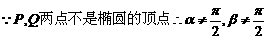
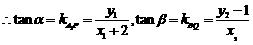 . …………………………………………10分
. …………………………………………10分
又因为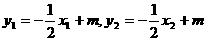 ,
,
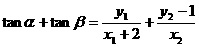
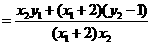
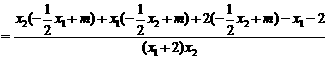
=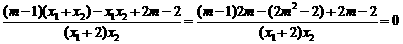
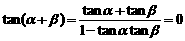 .
.
又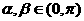
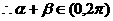
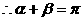 是定值.…………………………13分
是定值.…………………………13分
19.(本小题满分13分)
已知函数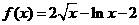 .(1)求
.(1)求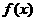 的单调区间;(2)若不等式
的单调区间;(2)若不等式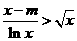
恒成立,求实数 的取值组成的集合.
的取值组成的集合.
解:(1)由已知得 .因为
.因为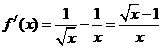 ,
,
所以当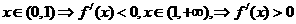 .
.
故区间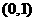 为
为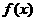 的单调递减区间,区间
的单调递减区间,区间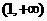 为
为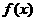 的单调递增区间.……5分
的单调递增区间.……5分
(2)①当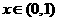 时,
时,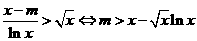 .
.
令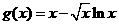 ,则
,则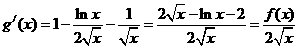 .
.
由(1)知当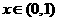 时,有
时,有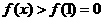 ,所以
,所以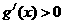 ,
,
即得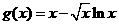 在
在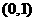 上为增函数,所以
上为增函数,所以 ,
,
所以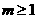 .
………………………………………………………………………………9分
.
………………………………………………………………………………9分
②当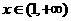 时,
时,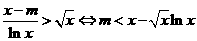 .
.
由①可知,当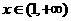 时,
时,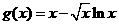 为增函数,所以
为增函数,所以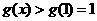 ,
,
所以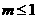 .
.
综合以上得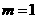 .故实数
.故实数 的取值组成的集合为
的取值组成的集合为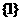 . …………………………13分
. …………………………13分
18.(本小题满分12分)
在一种智力有奖竞猜游戏中,每个参加者可以回答两个问题(题1和题2),且对两个问题可以按自己选择的顺序进行作答,但是只有答对了第一个问题之后才能回答第二个问题.假设:答对题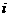 (
(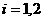 ),就得到奖金
),就得到奖金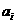 元,且答对题
元,且答对题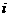 的概率为
的概率为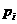 (
(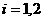 ),并且两次作答不会相互影响.
),并且两次作答不会相互影响.
(1)当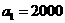 元,
元,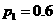 ,
,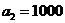 元,
元,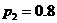 时,某人选择先回答题1,设获得奖金为
时,某人选择先回答题1,设获得奖金为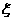 ,求
,求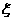 的分布列和
的分布列和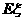 .
.
(2)若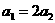 ,
,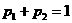 ,若答题人无论先回答哪个问题,答题人可能得到的奖金一样多,求此时
,若答题人无论先回答哪个问题,答题人可能得到的奖金一样多,求此时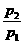 的值.
的值.
解:(1)分布列:
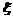 |
0 |
2000 |
3000 |
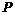 |
0.4 |
0.12 |
0.48 |
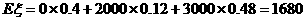 . ………………………………6分(2)设选择先回答题1,得到的奖金为
. ………………………………6分(2)设选择先回答题1,得到的奖金为 ;选择先回答题2,得到的奖金为
;选择先回答题2,得到的奖金为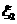 ,
,
则有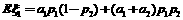 ,
,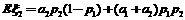 .根据题意可知:
.根据题意可知:
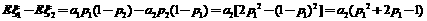 ,
,
当 时,
时,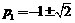 (负号舍去).当
(负号舍去).当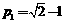 时,
时,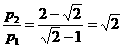 ,
,
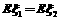 ,先答题1或题2可能得到的奖金一样多.………………………………12分
,先答题1或题2可能得到的奖金一样多.………………………………12分
17.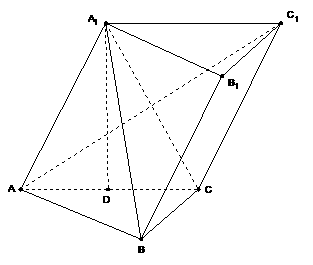 (本小题满分12分)
(本小题满分12分)
已知斜三棱柱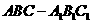 ,
,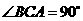 ,
,
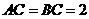 ,
, 在底面
在底面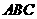 上的射影恰
上的射影恰
为 的中点
的中点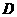 ,又知
,又知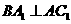 .
.
(1)求证: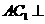 平面
平面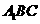 ;
;
(2)求二面角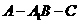 的大小.
的大小.
解:(1)取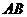 的中点
的中点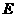 ,则
,则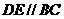 ,因为
,因为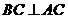 ,
,
所以 ,又
,又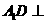 平面
平面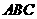 ,以
,以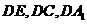 为
为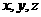 轴建立空间坐标系,则
轴建立空间坐标系,则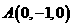 ,
, ,
,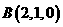 ,
,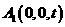 ,
,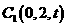 ,
,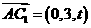 ,
,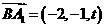 ,
,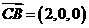 ,由
,由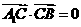 ,知
,知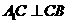 ,
,
又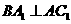 ,从而
,从而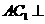 平面
平面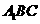 . …………………………………………6分
. …………………………………………6分
(2)由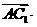
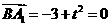 ,得
,得 .设平面
.设平面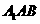 的法向量为
的法向量为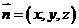 ,
,
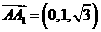 ,
,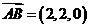 ,所以
,所以
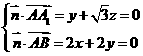 ,
,
设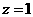 ,则
,则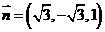 .
.
再设平面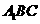 的法向量为
的法向量为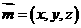 ,
,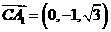 ,
,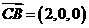 ,
,
所以 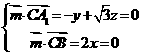 ,设
,设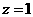 ,则
,则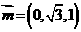 .
.
根据法向量的方向,可知二面角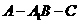 的大小为
的大小为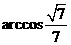 .
……………12分
.
……………12分
几何法(略)
16.(本小题满分12分)
已知sin(+3a) sin(-3a)=,a∈(0, ),求(1)求角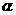 ;(2)求( -)sin4α的值.
;(2)求( -)sin4α的值.
解:(1)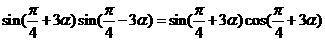
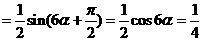 ,
,
即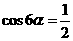 ,又6a∈(0,),∴
,又6a∈(0,),∴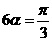 ,即
,即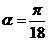 .…………………………6分
.…………………………6分
(2)(-)
sin4α=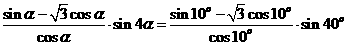
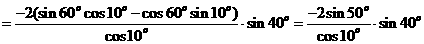
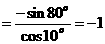 .………………………………………………………………………12分
.………………………………………………………………………12分
15.已知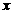 ,
,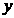 满足
满足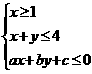 ,且目标函数
,且目标函数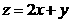 的最大值为7,最小值为4,
的最大值为7,最小值为4,
则(i)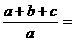
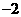 ;(ii)
;(ii)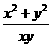 的取值范围为
的取值范围为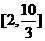 .
.
14.已知数列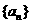 :1,1,2,1,1,3,1,1,1,4,1,1,1,1,5,…,
:1,1,2,1,1,3,1,1,1,4,1,1,1,1,5,…,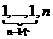 ,…….
,…….
(i) 对应的项数为
对应的项数为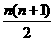 ;(ii)前2009项的和为
;(ii)前2009项的和为 .
.
13.底面边长为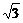 ,侧棱长为2的正三棱锥ABCD内接于球O,则球O的表面积为
,侧棱长为2的正三棱锥ABCD内接于球O,则球O的表面积为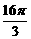 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com