
题目列表(包括答案和解析)
6.不等式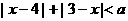 的解集为非空集合,则实数
的解集为非空集合,则实数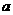 的取值范围是 ( )
的取值范围是 ( )
A.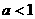 B.
B.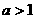
C.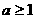 D.
D.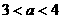
5.M( 为圆
为圆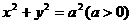 内异于圆心的一点,则直线
内异于圆心的一点,则直线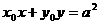 与该圆
与该圆
的位置关系为 ( )
A.相切 B.相交 C.相离 D.相切或相交
4.已知两点P(4,-9),Q(-2,3),则直线PQ与y轴的交点分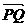 所成的比为( )
所成的比为( )
A.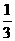 B.
B.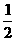 C.2 D.3
C.2 D.3
3.在等差数列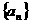 中,已知a3=2,则该数列的前5项和为 ( )
中,已知a3=2,则该数列的前5项和为 ( )
A.10 B.16 C.20 D.32
2.设向量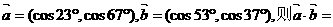 ( )
( )
A.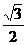 B.
B.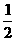 C.-
C.-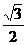 D.-
D.-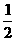
1.设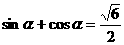 ,且
,且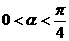 ,则
,则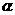 = ( )
= ( )
A.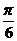 B.
B.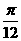 C.
C.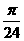 D.
D.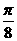
23. 附加题: (本小题满分5分, 但全卷不超过150分)
(1)a1 = a2 = 1, an+2 = a n +1 + an
(2) A=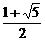 , B=
, B=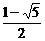 或A=
或A=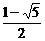 , B=
, B=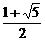
an = 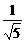 [(
[(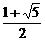 )n –(
)n –(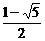 )n]
)n]
22. (本小题满分14分)
因为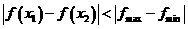 ,
,
函数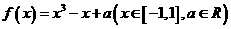 的导数是
的导数是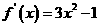 ,
,
当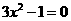 时,即
时,即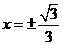 ,
,
当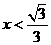 时,
时,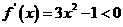 ;当
;当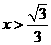 时,
时,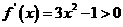 ,
,
故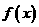 在
在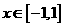 内的极小值是a -
内的极小值是a - 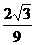 ;
;
同理, 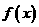 在
在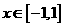 内的极大值是a+
内的极大值是a+ 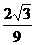 ;
;
因为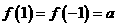 ,所以函数
,所以函数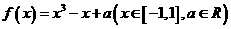 的最大值是a +
的最大值是a + 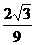 ,最小值是a -
,最小值是a - 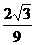 , 故
, 故 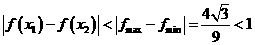 ,
,
所以函数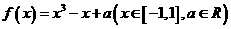 是“西湖函数”.
是“西湖函数”.
21. (本小题满分12分)
(1)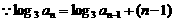 , 累加得
, 累加得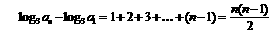 ,
,
∴ 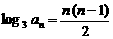 , 则
, 则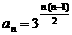 .
.
或者用累乘得 a n = 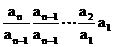 =
=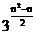 .
.
(2)∵ 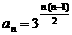 , ∴
, ∴ 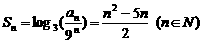 ;
;
而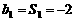 , 当
, 当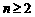 时,
时, 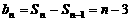 ,
, 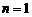 时也适合,
时也适合,
所以数列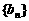 的通项公式为
的通项公式为 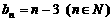 .
.
(3) 当 , 即
, 即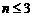 时,
时, 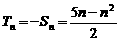 ,
,
当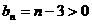 ,即n >3时,
,即n >3时,
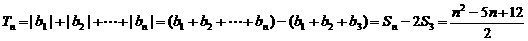 ,
,
综上所述 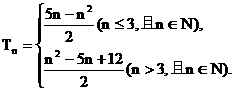 .
.
20. (本小题满分12分)
(1) 设圆周长为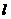 , 依题意有
, 依题意有 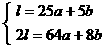 , 可表示为
, 可表示为 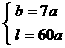 .
.
设出发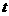 分钟后走完第三圈, 则
分钟后走完第三圈, 则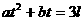 , 上式代入, 得
, 上式代入, 得
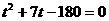 , ∵
, ∵ 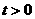 , ∴ 解得
, ∴ 解得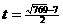 ,
,
所以走完第三圈需用时间为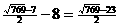 (分钟).
(分钟).
(2) 设出发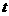 分钟后走完第
分钟后走完第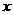 圈, 则
圈, 则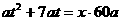 ,
,
解得 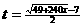 (分钟), 则走完
(分钟), 则走完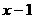 圈需
圈需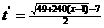 (分钟),
(分钟),
依题意应有 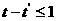 , 解此不等式, 得
, 解此不等式, 得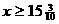 ,
,
所以, 从第16圈开始, 走一圈所用时间不超过1分钟.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com