
题目列表(包括答案和解析)
2.若向量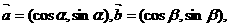 则
则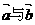 一定满足( )
A.
一定满足( )
A.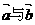 的夹角等于
的夹角等于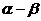 B.
B.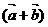 ⊥
⊥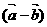
C.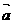 ∥
∥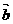 D.
D.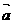 ⊥
⊥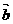
1.已知复数z1=1-i,z2=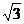 +i,则z=
+i,则z=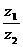 在复平面内对应点位于( )
在复平面内对应点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
(15)(本小题满分13分)
解关于x的不等式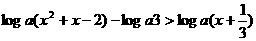 (a>0,a≠1)。
(a>0,a≠1)。
(16)(本小题满分13分)
设函数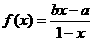 (x≠1,a>b)。
(x≠1,a>b)。
(I)求f(x)的反函数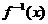 ;
;
(Ⅱ)判断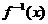 在(-b,+∞)上的单调性并用函数单调性定义加以证明。
在(-b,+∞)上的单调性并用函数单调性定义加以证明。
(17)(本小题满分14分)
某旅游点有50辆自行车供游客租赁使用,管理这些自行车的费用为每日115元。根据经验,若每辆自行车的日租金不超过6元,则自行车可以全部租出;若超过6元,则每超过1元,租不出去的自行车就增加3辆。
为了便于结算,每辆自行车的日租金x(元)只取整数,并且要求出租自行车一日总收入必须高于这一日的管理费用,用y(元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费后的所得)。
(I)求函数y = f(x)的解析式及其定义域;
(Ⅱ)试问当每辆自行车的日租金定为多少元时,才能使一日的净收入最多?
(必要时可参考以下数据: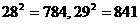 )。
)。
(18)(本小题满分14分)
如图,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆周上的一点,若A在PC,PB上的射影为D、E。
(Ⅰ)求证:AD⊥平面PBC;
(Ⅱ)若PA=AB=2,∠BPC=θ,试用tgθ表示△ADE的面积,当tgθ取何值时,△ADE面积最大,最大面积是多少?
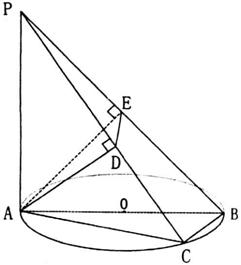
第(18)题图
(19)(本小题满分15分)
已知抛物线方程为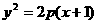 (p >0),直线l:x+y=m过抛物线的焦点F且被抛物线截得的弦长为3。
(p >0),直线l:x+y=m过抛物线的焦点F且被抛物线截得的弦长为3。
(Ⅰ)求p的值;
(Ⅱ)是否存在点M,使过点M的斜率不为零的任意直线与抛物线交于P、Q两点,并且以PQ为直径的圆恰过抛物线的顶点?若存在,求出M点的坐标;若不存在,请说明理由。
(20)(本小题满分15分)
若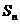 和
和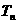 分别表示数列
分别表示数列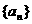 和
和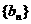 的前n项的和,对任意正整数n,
的前n项的和,对任意正整数n,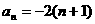 ,
,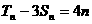 。
。
(Ⅰ)求数列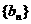 的通项公式;
的通项公式;
(Ⅱ)在平面直角坐标系内,直线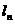 的斜率为
的斜率为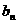 ,且与曲线
,且与曲线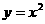 有且仅有一个交点,与y轴交于点
有且仅有一个交点,与y轴交于点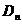 ,记
,记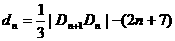 ,求
,求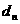 ;
;
(Ⅲ)若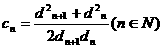 ,求证:
,求证: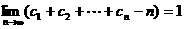 。
。
(11)已知椭圆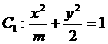 与
与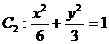 有相同的离心率e,那么m的值为___________.
有相同的离心率e,那么m的值为___________.
(12)设等差数列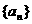 的前n项和为
的前n项和为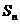 ,若
,若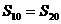 ,则
,则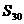 的值是_________。
的值是_________。
(13)如图,直三棱柱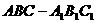 中,P、Q分别是侧棱
中,P、Q分别是侧棱 、
、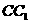 上的点,且
上的点,且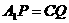 ,则四棱锥
,则四棱锥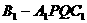 的体积与多面体
的体积与多面体 的体积的比值为________。
的体积的比值为________。
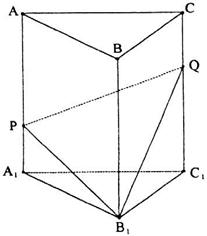
第(13)题图
(14)已知函数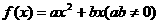 ,若
,若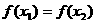 ,且
,且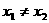 ,那么
,那么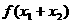 的值是_______________。
的值是_______________。
(1)下列集合中表示空集的是
(A){0} (B)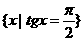
(C){x | ctgx = 0} (D)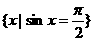
(2)(理)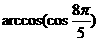 的值是
的值是
(A)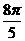 (B)
(B)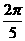
(C)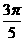 (D)
(D)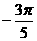
(文)已知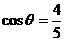 ,
,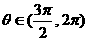 ,那么ctgθ的值等于
,那么ctgθ的值等于
(A)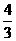 (B)
(B)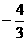
(C)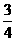 (D)
(D)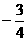
(3)已知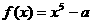 ,且f(-1)=0,那么
,且f(-1)=0,那么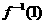 的值是
的值是
(A)0 (B)1
(C)-1 (D)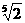
(4)(理)已知点A,B的极坐标分别是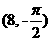 ,(8,
,(8,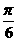 ),那么线段AB的中点C的极坐标可以是
),那么线段AB的中点C的极坐标可以是
(A)(4,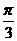 ) (B)(4,
) (B)(4,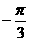 )
)
(C)(4,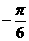 ) (D)(4,
) (D)(4,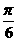 )
)
(文)若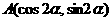 ,
,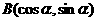 ,则A,B两点间的距离为
,则A,B两点间的距离为
(A)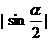 (B)
(B)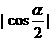
(C)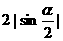 (D)
(D)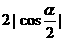
(5)将一张坐标纸折叠一次,使得点(0,2)与(-2,0)重合,且点(2002,2003)与点(m,n)重合,则m-n 的值为
(A)1 (B)-1
(C)0 (D)-2
(6)已知直线a、b和平面M、N,且a⊥M,那么
(A)b∥M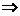 b⊥a (B)b⊥a
b⊥a (B)b⊥a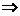 b∥M
b∥M
(C)N⊥M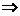 a∥N (D)
a∥N (D)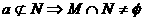
(7)从不同品牌的4台快译通和不同品牌的5台录音笔中任意抽取3台,其中至少要有快译通知录音笔各1台,则不同的取法共有
(A)140种 (B)84种
(C)70种 (D)35种
(8)若复数z与它的共轭复数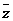 满足
满足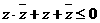 ,
,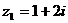 ,则
,则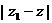 的最大值是
的最大值是
(A)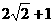 (B)
(B)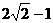
(C)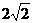 (C)2
(C)2
(9)若当P(m,n)为圆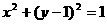 上任意一点时,不等式m+n+c≥0恒成立,则c的取值范围是
上任意一点时,不等式m+n+c≥0恒成立,则c的取值范围是
(A)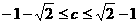 (B)
(B)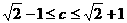
(C)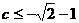 (D)
(D)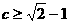
(10)已知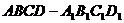 是棱长为a的正方体,P是
是棱长为a的正方体,P是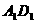 上的定点,Q是
上的定点,Q是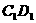 上的动点,长为b(b是常数,0 < b < a)的线段EF在棱AB上滑动,那么四面体PQEF的体积是
上的动点,长为b(b是常数,0 < b < a)的线段EF在棱AB上滑动,那么四面体PQEF的体积是
(A)常量 (B)变量且有最大值
(C)变量且有最小值 (C)变量且有最大值也有最小值
第Ⅱ卷(非选择题共100分)
22.(2003年高考江苏卷21)(本小题满分12分)
已知 为正整数.
为正整数.
(Ⅰ)设 ;
;
(Ⅱ)设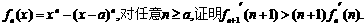
本小题主要考查导数、不等式证明等知识,考查综合运用所数学知识解决问题的能力,满分12分.
证明:(Ⅰ)因为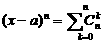
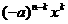 ,
,
所以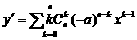
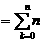
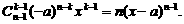
(Ⅱ)对函数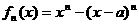 求导数:
求导数:
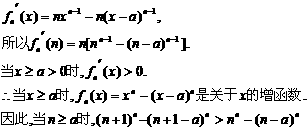
∴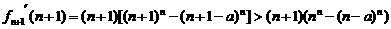
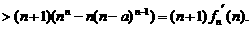
即对任意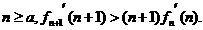
21.某商场预计全年分批购入每台价值为2000元的电视机共3600台。每批都购入x台,且每批均需付运费400元;贮存购入的电视机全年所付保管费与每批购入电视机的总价值(不含运费)成正比;若每批购入400台,则全年需用去运输和保管总费用43600元。现在全年只有24000元资金可以用于支付这笔费用。请问:能否恰当安排每批进货的数量使资金够用。写出你的结论,并说明理由。
解:设每批购入x台,由题意,全年需用保管费为 元;设全年运输和保管总费用为y元,则
元;设全年运输和保管总费用为y元,则
 。
。
由已知当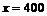 时,
时,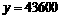 ,代入上式解之得
,代入上式解之得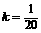
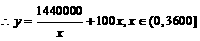
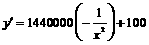 ,令
,令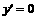 ,解之得
,解之得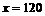 (台)
(台)
将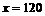 (台)代入,
(台)代入,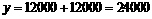 (元)
(元)
结果说明,只有安排每批进货120台,才能使所购资金够用。
20.(2003年高考全国卷-理19)(本小题满分12分)
已知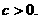 设
设
P:函数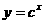 在R上单调递减.
在R上单调递减.
Q:不等式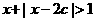 的解集为R,如果P和Q有且仅有一个正确,求
的解集为R,如果P和Q有且仅有一个正确,求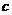 的取值范围.
的取值范围.
解:函数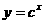 在R上单调递减
在R上单调递减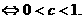
不等式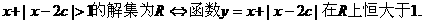

19.(2003年高考天津卷-理19)(本小题满分12分)
设 ,求函数
,求函数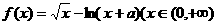 的单调区间.
的单调区间.
本小题主要考查导数的概念和计算,应用导数研究函数性质的方法及推理和运算能力. 满分12分.
解: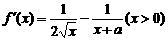 .
.
当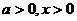 时
时 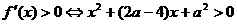 .
.
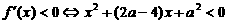
(i)当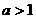 时,对所有
时,对所有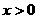 ,有
,有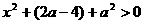 .
.
即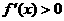 ,此时
,此时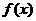 在
在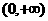 内单调递增.
内单调递增.
(ii)当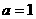 时,对
时,对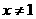 ,有
,有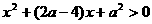 ,
,
即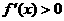 ,此时
,此时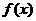 在(0,1)内单调递增,又知函数
在(0,1)内单调递增,又知函数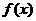 在x=1处连续,因此,
在x=1处连续,因此,
函数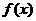 在(0,+
在(0,+ )内单调递增
)内单调递增
(iii)当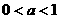 时,令
时,令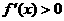 ,即
,即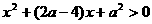 .
.
解得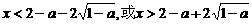 .
.
18.(2003年高考上海卷-理19)(本题满分14分)本题共有2个小题,第1小题满分5分,第2小题满分9分.
已知数列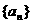 (n为正整数)是首项是a1,公比为q的等比数列.
(n为正整数)是首项是a1,公比为q的等比数列.
(1)求和: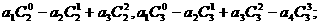
(2)由(1)的结果归纳概括出关于正整数n的一个结论,并加以证明.
[解](1)
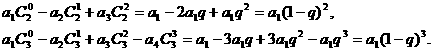
(2)归纳概括的结论为:
若数列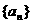 是首项为a1,公比为q的等比数列,则
是首项为a1,公比为q的等比数列,则
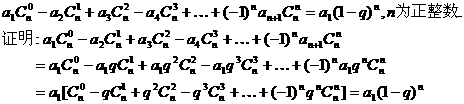
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com