
题目列表(包括答案和解析)
2. 已知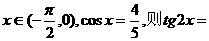 。
。
1.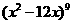 展开式中
展开式中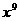 的系数是
的系数是
20.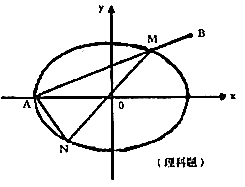 已知椭圆
已知椭圆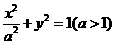 ,直线l过点A(-a,0)和点B(a,ta)(t>0)交椭圆于M。直线MO交椭圆于N。
,直线l过点A(-a,0)和点B(a,ta)(t>0)交椭圆于M。直线MO交椭圆于N。
(Ⅰ)用a,t表示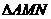 的面积S;
的面积S;
(Ⅱ)若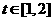 ,a为定值,求S的最大值。
,a为定值,求S的最大值。
解:(I)易得l的方程为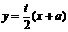 …1分 由
…1分 由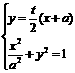 ,
,
得(a2t2+4)y2-4aty=0…2分
解得y=0或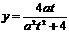 即点M的纵坐标
即点M的纵坐标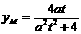 …………4分
…………4分
S=S△AMN=2S△AOM=|OA|·yM=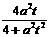 …7分 (2)由(1)得,
…7分 (2)由(1)得,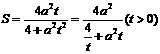
令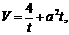 …………9分
…………9分
若1≤a≤2,则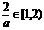 ,故当
,故当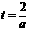 时,Smax=a…11分
时,Smax=a…11分
若a>2,则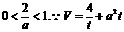 在[1,2]上递增,进而S(t)为减函数.
在[1,2]上递增,进而S(t)为减函数.
∴当t=1时,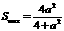 综上可得
综上可得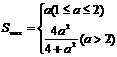 …………14分
…………14分
20.设数列{an}和{bn}满足a1=b1=6, a2=b2=4, a3=b3=3, 且数列{an+1-an }(n∈N*)是等差数列,数列{bn-2}(n∈N*)是等比数列.
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)是否存在k∈N*,使ak-bk∈(0,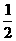 )?若存在,求出k;若不存在,说明理由.
)?若存在,求出k;若不存在,说明理由.
解:(I)由已知a2-a1=-2, a3-a2=-1, -1-(-2)=1
∴an+1-an=(a2-a1)+(n-1)·1=n-3
n≥2时,an=( an-an-1)+( an-1-an-2)+…+( a3-a2)+( a2-a1)+ a1
=(n-4)+(n-5) +…+(-1)+(-2)+6 =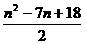
n=1也合适. ∴an=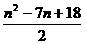 (n∈N*) ……………………3分
(n∈N*) ……………………3分
又b1-2=4、b2-2=2
.而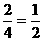 ∴bn-2=(b1-2)·(
∴bn-2=(b1-2)·(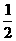 )n-1即bn=2+8·(
)n-1即bn=2+8·(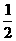 )n…6分
)n…6分
∴数列{an}、{bn}的通项公式为:an=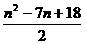 ,bn=2+(
,bn=2+(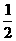 )n-3
)n-3
(II)设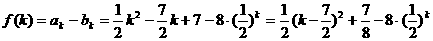
当k≥4时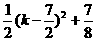 为k的增函数,-8·(
为k的增函数,-8·(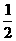 )k也为k的增函数,而f(4)=
)k也为k的增函数,而f(4)= 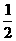
∴当k≥4时ak-bk≥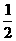 ………………10分
………………10分
又f(1)=f(2)=f(3)=0 ∴不存在k, 使f(k)∈(0,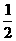 )…………12分
)…………12分
18.已知ABCD是矩形,PD⊥平面ABCD,PD=DC=a,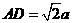 ,M、N分别是AD、PB的中点。
,M、N分别是AD、PB的中点。
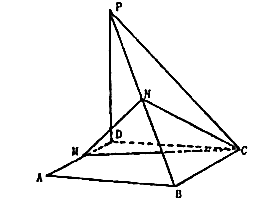 (Ⅰ)求证:平面MNC⊥平面PBC;
(Ⅰ)求证:平面MNC⊥平面PBC;
(Ⅱ)求点A到平面MNC的距离。
解:(I)连PM、MB ∵PD⊥平面ABCD
∴PD⊥MD…1分
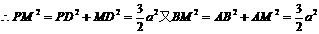
∴PM=BM 又PN=NB ∴MN⊥PB………3分
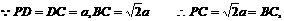
得NC⊥PB∴PB⊥平面MNC……5分
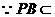 平面PBC
平面PBC
∴平面MNC⊥平面PBC……6分
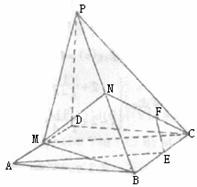 (II)取BC中点E,连AE,则AE//MC∴AE//平面MNC,
(II)取BC中点E,连AE,则AE//MC∴AE//平面MNC,
A点与E点到平面MNC的距离相等…7分
取NC中点F,连EF,则EF平行且等于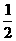 BN
BN
∵BN⊥平面MNC ∴EF⊥平面MNC,EF长为E
点到平面MNC的距离……9分 ∵PD⊥平面ABCD,
BC⊥DC ∴BC⊥PC.
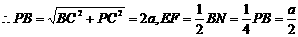
即点A到平面MNC的距离为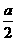 ……12分
……12分
17.已知函数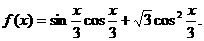
(Ⅰ)将f(x)写成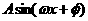 的形式,并求其图象对称中心的横坐标;
的形式,并求其图象对称中心的横坐标;
(Ⅱ)如果△ABC的三边a、b、c满足b2=ac,且边b所对的角为x,试求x的范围及此时函数f(x)的值域.
解:(Ⅰ)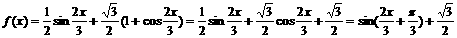 …3分
…3分
由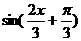 =0即
=0即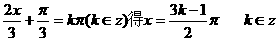
即对称中心的横坐标为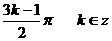 …………6分
…………6分
(Ⅱ)由已知b2=ac
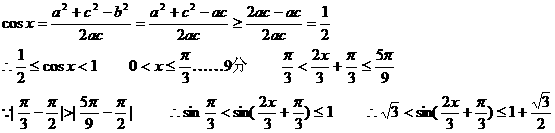 即
即 的值域为
的值域为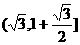
综上所述,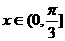
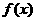 值域为
值域为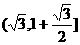 …………12分
…………12分
16.
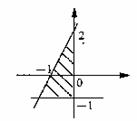 图中阴影部分可用哪一组二元一次不等式表示 ( C )
图中阴影部分可用哪一组二元一次不等式表示 ( C )
A.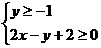 B.
B.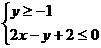
C.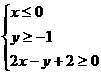 D.
D.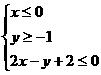
15.某商场开展促销奖活动,摇奖器摇出的一组中奖号码是6,5,2,9,0,4。参加
抽奖的每位顾客从0,1…,9这十个号码中抽出六个组成一组。如果顾客抽出的
方个号码中至少有5个与摇奖器摇出的号码相同(不计顺序)就可以得奖,某位
顾客可能获奖的概率为 ( D )
(A)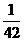 (B)
(B)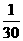 (C)
(C)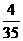 (D)
(D)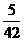
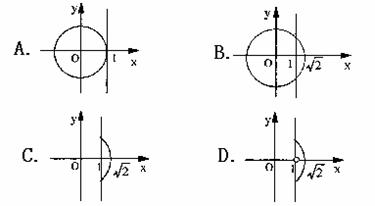
14.方程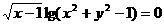 所表示的曲线图形是 ( D )
所表示的曲线图形是 ( D )

13. 若某等差数列{an}中,a2+a6+a16为一个确定的常数,则其前n项和Sn中也为
确定的常数的是 ( B )
A.S17 B.S15 C.S8 D.S7
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com