4.29 巧手剪裁

　　 你能将一个边长为12厘米的正方形分成一些小正方形吗？(所分成的小正方形的边长必须是整数厘米，大小可以不相同)现限定所分成的小正方形的个数不超过12，请设计一些不同的分法。

[分析与参考答案]

　 将一个边长为12厘米的大正方形分成一些边长为整数厘米的小正方形，最简单的是平均分。也就是将大正方形分成边长分别是1厘米、2厘米、3厘米、4厘米、6厘米的小正方形，边长和个数的关系可以从下面这张表中看出来：

如果限定所分成的小正方形个不超过12，下面是一些不同分法的例子：(以所分成的小正方形中最大的一个的边长的长短为序)

设所分成的小正方形中最大的一个的边长为n厘米。

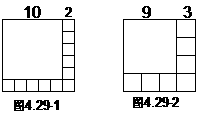(1)当n＝10时，例：(图4.29-1)

　　 (2)当n＝9时，例：(图4.29-2)

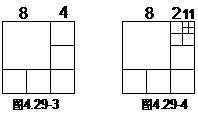　　 (3)当n＝8时，例：(图4.29-3，图4.29-4)

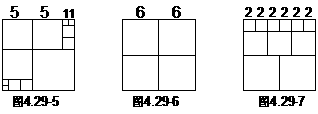　　 (4)当n＝7时，例：(图4.29-5，)

　　 (5)当n＝6时，例：(图4.29-6，图4.29-7)

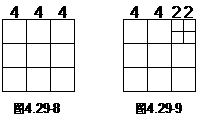　　 (6)当n＝9时，例：(图4.29-8，图4.29-9)

以上我们仅仅是举了一些例子，实际上不同的分法还更多。亲爱的读者：你还能想出几种其它的分法吗？

4.28 巧拼台布

小明家有两块正方形的台布，边长都是1米。最近小明家新买了一张边长是1.3米的正方形的新桌子，两块台布都不合适用了，丢掉又太可惜。你能替小明想个办法，使两块台布拼成一块正方形大台布(布料没有剩余)，盖住现在的新桌子吗？试一试。

[分析与参考答案]

　两块边长是1米的正方形台布，面积的总和是2平方米，新桌子的边长1.3米，面积是1.69平方米，两块台布拼起来应该能盖住新桌子。我们知道正方形的对角线比正方形的边长要长，因此，如果能沿着原来的正方形对角线剪开，通过适当的拼合以后，使得正方形新台布的边长是原来正方形的对角线的长度，这样就有可能盖住新桌子。根据这样的思路，有以下一些拼法：

　方法一：如图4.28-1所示，把其中一块台布沿两条对角线剪开，可以得到四个相等的等腰直角三角形，再把它们缝在另一块台布的四边上面，就可以得到一块新的正方形大台布。

　　　　　　　　　　　　　　　　 图4.28-1

　　 方法二：如图4.28-2所示，把两块台布都按一条对角线剪开，就可以得到四块大小相同的三角形台布，再把它们按直角边缝起来，就成了一块正方形大台布了。

　　　　　　 　　　　　　　　　图4.28-2

　 　方法三：如图4.28-3所示，把两块台布都沿着两条对角线剪开，就可以得到八块大小相同的三角形台布，再把它们两块一组沿斜边缝起来，就组成了四块大小相同的正方形台布，最后把它们缝成正方形大台布。　

　　　　 　　　　　　　　　　　　图4.28-3

　　 如果把两块小正方形台布平均分成更多更小的等腰直角三角形，那么也可以拼成大正方形台布。

4.27 可爱的小猫

图4.27-1中有10行10列共有100只各不相同的小猫，一个同学默默地选择了一只自己喜欢的小猫，并暗暗记住了这只小猫的位置，不告诉其他同学。让另一个同学猜，他记住的这只小猫的位置在哪里，暗暗记住小猫位置的同学要回答“是”或者“不是”。

　　　　　　　　　　　　　　 图4.27-1

　例如：一个同学默默地选了位于从左往右数第三列，从下往上数第三行的这只小猫。

　　　　 猜的同学问　　　　　　　　 记的同学答　　　

小猫在从左往右数第5列的右面？　　　 不是。 　　　　

小猫在从上往下数第4行的下面？　　　 是。　　　　

小猫在从上往下数第5行的下面？　　　 是。　　　　

小猫在从左往右数第3列的右面？　　　 不是。　　　

小猫在从左往右数第2列的右面？　　　 是。　　　

你喜欢的小猫的位置肯定在从下往

上数的第3行，从左往右数第3列？　　 是。　

[分析与参考答案]

　　 我们可以先确定小猫在第几行后，再来确定小猫在第几列。每提一个问题能排除的小猫越多越好，我们如果提问“小猫在上面5行”，肯定就可以排除其中的5行，如果确定小猫在下面6-10行，我们可以提问“小猫在第8行以下(即9，10两行)”，这样又能排除其中的两行或三行。再以这样的方法继续问下去，直至剩下一行。确定列的方法也可以一样。(请参考第1-3年级册第2.51题的答案)

　　 亲爱的同学，请与你的同学或长辈一起，做一次猜小猫的游戏。

4.26 集中货物

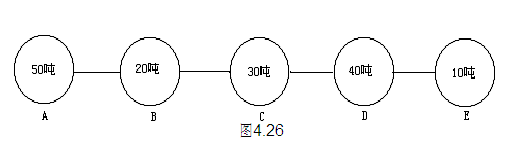
　 如图4.26，在公路上有A，B，C，D，E五个仓库，每个仓库之间的距离均为10千米，各自存放着一些货物(重量如图4.35所示)，如果要把B仓库中的20吨货物运往A仓库，我们把货物的重量20吨与运输的路程10千米的乘积20吨×10千米=200吨千米，称为运输量。现在要把四个仓库里的货物集中到一个仓库里去，有哪些运输方案，哪一个方案运输总量最少？

[分析与参考答案]

　要把货物集中到一个仓库，这个仓库可以是A，B，C，D，E五个仓库的任何一个中，下面我们逐一来计算运输总量。

(1)集中到A仓库，总运输量为：

20×10+30×(10×2)+40×(10×3)+10×(10×4)=2200(吨千米)

(2)集中到B仓库里，总运输量为：

50×10+30×10+40×(10×2)+10×(10×3)=1900(吨千米)

(3)集中到C仓库里，总运输量为：

50×(10×2)+20×10+40×10+10×(10×2)=1800(吨千米)

(4)集中到D仓库，总运输量为：

50×(10×3)+20×(10×2)+30×10+10×10=2300(吨千米)

(5)集中到E仓库中，总运输量为：

50×(10×4)+20×(10×3)+30×(10×2)+40×10=3600(吨千米)

经过比较上面五种方案中，第3个方案总运输量最少。

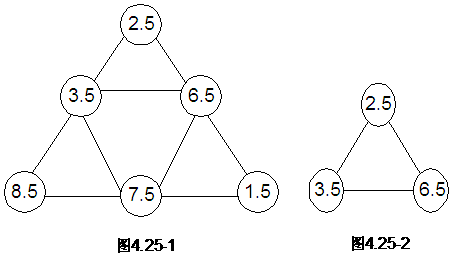
6.5+7.5+1.5=15.5　 2.5+8.5+1.5=12.5

2.5+3.5+6.5=12.5　 3.5+6.5+7.5=17.5　 8.5+3.5+7.5=19.5　　　　 　　

4.25　 三个数的和

　　　 求出下图4.25-1中三角形三个顶点上数的和。

[分析与参考答案]

　　 像图4.25-2这个三角形，2.5，3.5，6.5这三个数是三角形三个顶点上的数，它们的和是2.5+3.5+6.5=12.5.。在图4.25-1中，小的三角形有四个，大的三角形有一个，共有五个三角形，相应的五个算式如下：

4.24 奇妙四位数

　　 在四位数中，有些数满足四个数字的积等于这四个数字中一个。如1119,1×1×1×9=9，你能写出这样的四位数吗？试一试。

[分析与参考答案]

　　 根据题意，如果所求的四位数四个数字的乘积是零，那么对于这样的四位数只要其中有一个数字是0，其余三个数字可以是任意的，如1110，1009，9009，对于这样的四位数我们可以轻松的写出许多个。下面我们考虑乘积不是零的情况，由于四个数字相乘的积是其中一个数字，因此，这四个数字中必有三个数字是1，另一个数字可以是1，2，…，9中的一个。

　 (1) 1111

　 (2)1112　　 1121　　 1211　　 2111

　 (3)1113　　 1131　　 1311　　 3111　　

　　 　　　　　　……　　　　　　　　　　　　　　　　　

　 (9)1119　　 1191　　 1911　　 9111

积不是0，满足条件的四位数共有1+4×8=33个。

4.23 画15°角

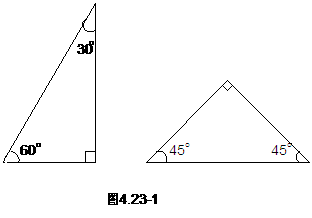　　 小芳在做作业时要画一个15°的角,但她只有两块三角板(如图4.23-1),怎样利用两块三角板画15°的角呢?请你帮帮小芳。

[分析与参考答案]

　 直接利用两特殊角的差，画15°角。

(1)利用45°－30°=15°，可以先用三角形画出一个45°的角，然后在这个45°的角内作出一个30°的角，这两个角的差就是15°。如图4.23-2。

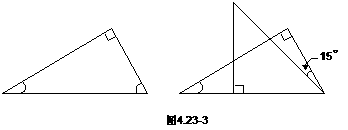
(2)利用60°－45°=15°，可以先作出一个60°的角，然后在这个角的内部作一个45°的角，，这两个角的差就是15°。见图4.23-3。

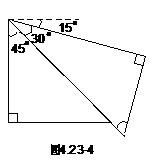
(3)90°－(45°+30°)=15°，作图过程与(1)(2)类似。见图4.23-4。

(4) 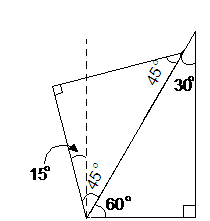60°+45°-90°=15°，作图过程与(1)(2)类似。见图4.23-5。

　　　　　　　　　　　　　 图4.23-5

4.22 走迷宫

　　 游园会布置了一个数学迷宫(如图4.28)，迷宫是由一些互相连通的房间布置而成的，每一个房间里都有一个数。迷宫的入口在1号房间，出口在9号房间，如果要求走迷宫的同学只经过五个房间从入口走到出口，把这五个房间里的数相加，得到的和就是这位同学的分数，他可凭分数去总台领奖品，分数越大，奖品越好。如果规定一个房间只能进入一次，那么怎样从入口走到出口？得到的和是多少？如果有一位同学去总台领奖时，他的分数是33分，总台是否应该给他分值是33分的奖品？　　　

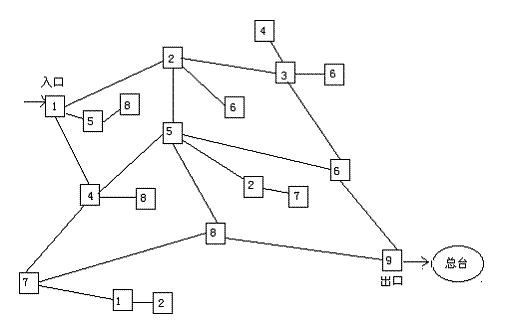　　　 　　　　　　　　　　　　　图4.22

[分析与参考答案]

　　 观察迷宫，我们会发现沿某些路线走，不能到达出口，只能到达某一个房间。因此要走出迷宫就不能选择这些路线。例如从1号房间出发，不能先走到有数字5的那个房间，只可以向下走4号房间或者向右走2号房间。由于不能重复走，且只能经过五个房间，所以不能走回头路，一定要往下走或往右走。可以得到以下几种行走路线：

　　　　　　　　 14789　　 和29

　　　　　　　　 14589　　 和27

　　　　　　　　 14569　　 和25

　　　　　　　　 12589　　 和25

　　　　　　　　 12569　　 和23

　　　　　　　　 12369　　 和21

　　 从上面的行走路线可以看出，共有6种行走路线，但得到的分值只有5种，有一种是重复的。

只经过五个房间，且不重复，得到的最高分数是29分，不可能出现33分，所以总台不能发给这位同学奖品。

如果只要求行走的路线不重复，而经过的房间个数不限，你能得到哪些分数？你能把行走路线写出来吗？