7、饲养场共养4800只鸡，母鸡只数比公鸡只数的1．5倍还多300只，公鸡、母鸡各养了多少只?　

6、甲车每小时行48千米，乙车每小时行56千米，两车从相距12千米的两地同时背向而行，几小时后两车相距272千米?　 [4]

5、一匹布长36米，裁了10件大人衣服和8件儿童衣服，每件大人衣服用布2．4米，每件儿童衣服用布多少米?　 　

4、化肥厂用大、小两辆汽车运47吨化肥，大汽车运了8次，小汽车运了6次正好运完，大汽车每次运4吨，小汽车每次运多少吨?　 [3]

3、洗衣机厂今年每日生产洗衣机260台，比去年平均日产量的2．5倍少40台，去年平均日产洗衣机多少台?　 [3]

2、学校今年绿化面积1800平方米，比去年的绿化面积的2倍还多40平方米，去年绿化面积是多少平方米?　 [3]

1、25除以一个数的2倍，商是3余1，求这个数．　 [4]

4.40 搭三角形

　 　有一批长度分别为1，2，3，4，5，6，7，8，9，10厘米的细木条，(它们的数量都足够多)，请你选出三根木条作为三条边，围成一个三角形，并要求其中一条边长为10厘米，你能围出哪些不同的三角形？

[分析与参考答案]

　 　三角形有三条边，有一条已经确定为10厘米，另两条边的和一定要大于10厘米。

　　 方法一：三角形按边分可以分为三类：等边三角形、等腰三角形、不等边三角形。 按这样的分类标准，可以得到以下几种三角形：

　　 等边三角形；三条边都用10厘米长的木条

　　 等腰三角形；由于已经有一条边长为10厘米，这条边长如果作为等腰三角形的腰，那么等腰三角形的两条腰长都是10厘米，底边长可以是1厘米，2厘米，… ，9厘米；也可以把已知的10厘米长的这条边作为底，那么两条腰长可以都是6厘米，7厘米，8厘米和9厘米。具体构成方案见下表： (单位：厘米)

不等边三角形 。由于是不等边三角形，因此在已经确定是一条边为10厘米的情况下，可以考虑第二条边长为9厘米。当确定第二条边长为9厘米后，第三条边长可以是2厘米，3厘米，…，8厘米；用类似的方法可以确定第三条边长为8厘米，7厘米和6厘米的各种情况。具体的构成方案见下表：(单位：厘米)

　　 由此可得到30个不同的三角形。(1+13+16=30)

　　 方法二：第一条边长10厘米已经完全确定，我们可以从第二条边长开始考虑。看一看第二条边长是10厘米时，可以构成哪些三角形，当第二条边长是9厘米时，又可以构成哪些三角形，即从10厘米起依次缩短，也可以得到所有三角形：

　　 第二条边长为10厘米；可构成的三角形如下：(单位：厘米)

　 类似的：

　　 第二条边长为9厘米；可构成8个三角形。

　　 第二条边长为8厘米；可构成6外三角形。

　　 第二条边长是7厘米；可构成4个三角形。

　　 第二条边长是6厘米；可构成2个三角形。　　 由此也可以得到30个不同的三角形 。(10+8+6+4+2=30)

4.39 称出次品

　　 有8 个大小完全一样的球，其中 一个是次品，已经知道次品球比其它球稍轻一些。用一架没有砝码的天平，称几次可以找到这个次品球？

[分析与参考答案]

　　 从题目中已经知道次品球比其它球稍轻一些，这架天平没有砝码，因此有许多不同的方法，方法不同称的次数就不同。

　　 方法一：在8个球中任意地选出一个，放到天平的一边，另外的球一个一个地放在天平的另一边，这样最多称6 次就能找到这个次品球。

　　 方法二：把8 个球平均分成四堆，每堆两个。把每一堆的两个球分别放在天平的左右两边。这样最多称4次就能找到这个次品球。

方法三：把8 个球分成三堆，其中的两堆各三个，另一堆为两个。在天平两边各放3个球，如果左右平衡，那么剩下一堆的两个球再称一次就到找到这个次品球，共称2次。如果两边各放三个球时，天平的左右不平衡，那么轻的一边的三个球中必有一个次品球。在这堆含有次品球的三个球中再取出两个称一次，无论天平是否平衡，都能找到这个次品球，这样一共也只称两次。

4.38 构成三角形

张明在纸上画了四个点，如果把这四个点彼此连接连成一个图形。这个图形中有几个三角形？

[分析与参考答案]

　　 把张明在纸上画的四个点彼此连接后形成一个图形，这个图形的形状与这四个点的位置关系很大。可以分以下四种情况：

　　　 ⑴四点在一条直线上。这时不能形成三角形，见图4.38-1。

　　　 ⑵三点在一条直线上，另一点在这条直线以处，这时三角形的个数是3， 见图4.38-2。

　　　 ⑶把其中的三点连接组成一个三角形，另一点在这个三角形的内部，这时三角形的个数是4， 见图4.38-3。

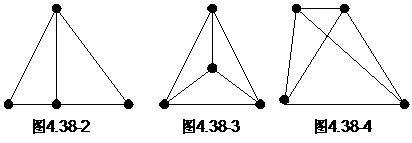　　 　　⑷把其中的三点连接组成一个三角形，另一点在这个三角形的外部，这时三角形的个数是8， 见图4.38-4。