
题目列表(包括答案和解析)
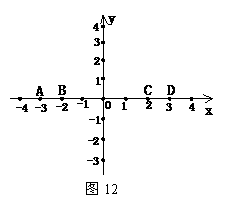 21,如图10所示的直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0,0),B(3,6),C(14,8),D(16,0),确定这个四边形的面积.
21,如图10所示的直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0,0),B(3,6),C(14,8),D(16,0),确定这个四边形的面积.
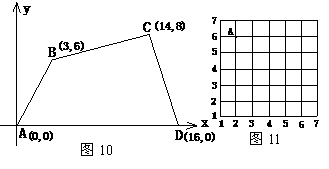
22,如图11所示,A的位置为(2,6),小明从A出发,经(2,5)→(3,5)→(4,5)→(4,4)→(5,4)→(6,4),小刚也从A出发,经(3,6)→(4,6)→(4,7)→(5,7)→(6,7),则此时两人相距几个格?
23,如果│3x+3│+│x+3y-2│=0,那么点P(x,y)在第几象限?点Q(x+1,y-1)在坐标平面内的什么位置?
24,如图12所示,C、D两点的横坐标分别为2,3,线段CD=1;B、D两点的横坐标分别为-2,3,线段BD=5;A、B两点的横坐标分别为-3,-2,线段AB=1.
(1)如果x轴上有两点M(x1,0),N(x2,0)(x1<x2),那么线段MN的长为多少?
(2)如果y轴上有两点P(0,y1),Q(0,y2)(y1<y2),那么线段PQ的长为多少?
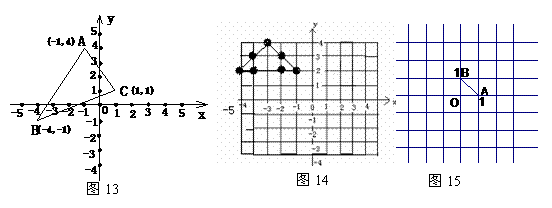
25,如图13,三角形ABC中任意一点P(x0,y0),经平移后对称点为P1(x0+3,y0-5),将三角形作同样平移得到三角形A1B1C1,求A1、B1、C1 的坐标, 并在图中画出A1B1C1的位置.
26,如图14将图中的点(一5,2)(一3,3)(一1,2)(一4,2)(一2,2)(一2,0)(一4,0)做如下变化:
(1)横坐标不变,纵坐标分别减4,再将所得的点用线段依次连接起来,所得的图形与原来的图形相比有什么变化?
(2)纵坐标不变,横坐标分别加6,再将所得的点用线段依次连接起来,所得的图形与原来的图形相比有什么变化?
27,如果将点P绕定点M旋转180°后与点Q重合,那么称点P与点Q关于点M对称,定点M叫做对称中心.此时,M是线段PQ的中点.如图15,在直角坐标系中,△ABO的顶点A、B、O的坐标分别为(1,0)、(0,1)、(0,0).点列P1、P2、P3、…中的相邻两点都关于△ABO的一个顶点对称:点P1与点P2关于点A对称,点P2与点P3关于点B对称,点P3与P4关于点O对称,点P4与点P5关于点A对称,点P5与点P6关于点B对称,点P6与点P7关于点O对称,…….对称中心分别是A、B,O,A,B,O,…,且这些对称中心依次循环.已知点P1的坐标是(1,1),试求出点P2、P7、P100的坐标.
11,已知点M(a,b),且a·b>0,a+b<0,则点M在第___象限.
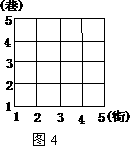
12,如图4所示,从2街4巷到4街2巷,走最短的路线的走法共有___种.
13,如图5所示,进行“找宝”游戏,如果宝藏藏在(4,5)字母牌的下面,那么应该在字母___的下面寻找.
14,点P(a,b)与点Q(a,-b)关于___轴对称;点M(a,b)和点N(-a,b) 关于___轴对称.
15,△ABC中,A(-4,-2),B(-1,-3),C(-2,-1),将△ABC先向右平移4个单位长度,再向上平移3个单位长度,则对应点A′、B′、C′的坐标分别为___、___、___.
16,已知点M(-4,2),将坐标系先向下平移3个单位长度,再向左平移3个单位长度,则点M在新坐标系内的坐标为___.
17,在一座共8层的商业大厦中,每层的摊位布局基本相同.小明的父亲在6楼的位置如图3所示,其位置可以表示为(6,2,3).若小明的母亲在5楼,其摊位也可以用如图6表示,则小明的母亲的摊位的位置可以表示为___.

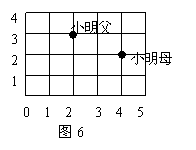
18,观察图象,与如图7中的鱼相比,图5中的鱼发生了一些变化.若图7中鱼上点P的坐标为(4,3.2),则这个点在如图8中的对应点P1的坐标为___(图中的方格是1×1).
19,长方形ABCD中,A、B、C三点的坐标分别是A(6,4),B(0,4),C(0,0)则D点的坐标是 .
20,如图9在一个规格为4×8的球台上,有两个小球P和Q,设小球P的位置用(1,3)表示,小球Q的位置用(7,2)表示,若击打小球P经过球台的边AB上的点O反弹后,恰好击中小球Q,则O点的位置可表示为 .
1,点P(m +3,m +1)在直角坐标系的x轴上,则P点坐标为( )
A.(0,-2) B.(2,0) C.(0,2) D.(0,-4)
2,在直角坐标系xOy中,已知A(2,-2),在y轴上确定点P,使△AOP为等腰三角形,则符合条件的点P共有( )
A.2个 B.3个 C.4个 D.5个
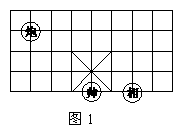
3,如图1所示的象棋盘上,若帅位于点(1,-2)上,相位于点(3,-2)上,则炮位于点( )
A.(-1,1) B.(-1,2) C.(-2,1) D.(-2,2)
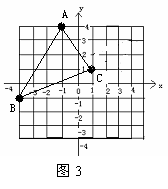
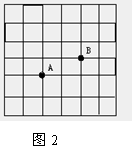
4,(2008山东滨州)在平面直角坐标系中,若点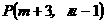 在第四象限,则m的取值范围为(
)
在第四象限,则m的取值范围为(
)
A、-3<m<1 B、m>1 C、m<-3 D、m>-3
5,已知坐标平面内三点A(5,4),B(2,4),C(4,2),那么△ABC的面积为( )
A.3 B.5 C.6 D.7
6,小明家的坐标为(1,2),小丽家的坐标为(-2,-1),则小明家在小丽家的( )
A.东南方向 B.东北方向 C.西南方向 D.西北方向
7、已知如图2中方格纸中的每个小方格是边长为1的正方形,A、B两点在小方格的顶点上,位置分别用(2,2)、(4,3)来表示,请在小方格的顶点上确定一 点C,连结AB,AC,BC,使△ABC的面积为2平方单位.则点C的位置可能为( )
A.(4,4) B.(4,2) C.(2,4) D.(3,2)
8,如图3,若△ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+5,y0-3)那么将△ABC作同榉的平移得到△A1B1C1,则点A的对应点A1的坐标是( )
A.(4,1) B.(9,一4) C.(一6,7) D.(一1,2)
9,已知点A(2,0)、点B(-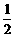 ,0)、点C(0,1),以A、B、C三点为顶点画平行四边形.则第四个顶点不可能在( )
,0)、点C(0,1),以A、B、C三点为顶点画平行四边形.则第四个顶点不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10,已知点A(0,-1),M(1,2),N(-3,0),则射线AM和射线AN组成的角的度数( )
A.一定大于90° B.一定小于90° C.一定等于90° D.以上三种情况都有可能
如果│3x-13y+16│+│x+3y-2│=0,那么点P(x, y)在第几象限?点Q(x+1,y-1)在坐标平面内的什么位置?
 七、中考题与竞赛题:(共16分)
七、中考题与竞赛题:(共16分)
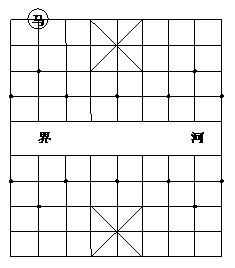
如图4所示,图中的 能走遍棋盘中的任何一个位置吗?若不能,指出哪些位置
能走遍棋盘中的任何一个位置吗?若不能,指出哪些位置 无法走到;若能,请说明原因.
无法走到;若能,请说明原因.
如图所示,C,D两点的横坐标分别为2,3,线段CD=1;B,D两点的横坐标分别为-2,3,线段BD=5;A,B两点的横坐标分别为-3,-2,线段AB=1.
(1)如果x轴上有两点M(x1,0),N(x2,0)(x1<x2),那么线段MN的长为多少?
(2)如果y轴上有两点P(0,y1),Q(0,y2)(y1<y2),那么线段PQ的长为多少?
如果点A(t-3s,2t+2s),B(14-2t+s,3t+2s-2)关于x轴对称,求s, t的值.
如果点A的坐标为(a2+1,-1-b2),那么点A在第几象限?为什么?
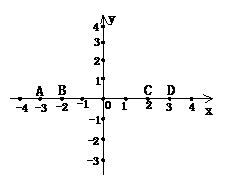
1.如图1所示,点A的坐标是 ( )毛
A.(3,2); B.(3,3); C.(3,-3); D.(-3,-3)
2.如图1所示,横坐标和纵坐标都是负数的点是 ( ) A.A点 B.B点 C.C点 D.D点
3.如图1所示,坐标是(-2,2)的点是 ( )
A.点A B.点B C.点C D.点D
4.若点M的坐标是(a, b),且a>0,b<0,则点M在( )
A.第一象限;B.第二象限;C.第三象限;D.第四象限
 二、填空题:(每小题3分,共15分)
二、填空题:(每小题3分,共15分)
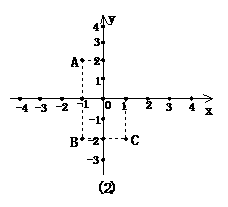
1.如图2所示,点A的坐标为_______,点A关于x轴的对称点B的坐标为______, 点B关于y轴的对称点C的坐标为________.
2.在坐标平面内,已知点A(4,-6),那么点A关于x轴的对称点A ′的坐标为_____,点A关于y轴的对称点A″的坐标为_______.
3.在坐标平面内,已知点A(a, b),那么点A关于x轴的对称点A ′的坐标为______,点A关于y轴的对称点A″的坐标为_____.
4.点A(-3,2)在第_______象限,点D(-3,-2)在第_______象限,点C( 3, 2) 在第______象限,点D(-3,-2)在第_______象限,点E(0,2)在______轴上, 点F( 2, 0) 在______轴上.
5.已知点M(a, b),当a>0,b>0时,M在第_______象限;当a____, b______时,M 在第二象限;当a_____, b_______时,M在第四象限;当a<0,b<0时,M在第______象限.
2.计算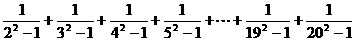
七年级数学 第 4 页 共 1 页
2007-2008学年度第一学期期中考试
1. 有一列数按一定规律排列为1,-3,5,-7,9,…,如果其中三个相邻的数之和为-201,求这三个数?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com