1.6a²-2ab-2(3a²+ab)的结果是(　　 )

A.-3ab　　　　 B.-ab　　　　 C.3a²　　　　 D.9a²

答案：A

5.计算下列各题：

(1)(-3)²-(-2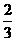)³÷(-)³；

(2)(-1)·(-1)²·(-1)³……(-1)⁹⁹·(-1)¹⁰⁰.

思路解析：由乘方的符号法则，易知对于一个有理数a，有(-a)²ⁿ=a²ⁿ，(-a)²ⁿ⁺¹=-a²ⁿ⁺¹(n为整数).本例应依此先确定幂的符号，再进行乘方运算.

答案：(1)-18;　 (2)-1.

成功的秘诀

一位演员巡回演出回来，他对朋友说：“我获得了极大的成功，我在露天广场上演出时，观众的掌声经久不息.”

“你真走运，”他的朋友说，“下个星期再演出时就要困难一些了.”

“为什么？”演员问.

“天气预报说下周要降温，这样蚊子会少多了.”那人回答.

30分钟训练(巩固类训练，可用于课后)

4.计算：

(1)(-1)¹⁰⁰；　　 (2)(-1)¹⁰¹；　　 (3)(-0.2)³；　　 (4)(+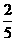)³；

(5)(-)⁴；　　 (6)(+0.02)².

思路解析：根据乘方的定义进行计算.

答案：(1)1;　 (2)-1;　 (3)-0.008;　 (4)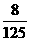;　 (5)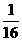;　 (6)0.000 4.

3.计算：

(1)(－6)⁴；　　 (2)－6⁴；　　 (3)(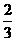－)⁴；　　 (4)－.

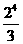思路解析：本题中(－6)⁴表示4个－6相乘，－6⁴表示6⁴的相反数，切不可看成同样的，且结果互为相反数.(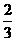－)⁴表示4个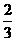－相乘，而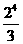－表2⁴除以3的商的相反数.要注意区别.

答案：(1)1 296;　 (2)－1 296;　 (3)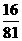;　 (4)－.

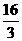2.判断题：

(1)-5²中底数是-5，指数是2；　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

(2)一个有理数的平方总是大于0；　　　　　　　　　　　　　　　　　　　　 (　　 )

(3)(-1)^{2 001}+(-1)^{2 002}=0；　　　　　　　　 　　　　　　　　　　　　　　　(　　 )

(4)2×(-3)²=(-6)²=36;　　　　　　　　　　　　　　　　 　　　　　　　　　　(　　 )

(5) = .　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

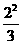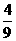思路解析：区别底的符号与幂结果的符号，注意底数是负数和分数时要把该底数用小括号括起来.

答案：(1)×　 (2)×　 (3)×　 (4)×　 (5)×

1.把下列各式写成幂的形式，并指出底数、指数各是什么？

(1)(-1.2)×(-1.2)×(-1.2)×(-1.2)×(-1.2);

(2) ×××××;

(3).

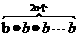思路解析：底数是负数或分数时，要用括号将底数括起来，在括号外边写上指数，如(-1.2)⁵不能写成-1.2⁵，()⁶不能写成.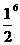

答案： (1) (-1.2)⁵，其中底数是-1.2，指数是5;

(2) ()⁶，其中底数是，指数是6;

(3)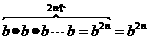，底数是b，指数是2n.

2.把下列各式写成幂的形式，并指出底数是什么?指数是什么?

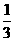(1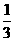)(－1)(－1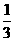)(－1)(－1);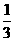

(2)(－0.1)×(－0.1)×(－0.1).

思路解析：根据幂的意义写出.

答案：(1)(－1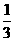)⁴，底数是－1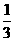，指数是4;

(2)(－0.1)³，底数是－0.1，指数是3.

10分钟训练(强化类训练，可用于课中)

1.填空题

(1)求几个相同因数的积的运算，叫做_______，即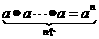 =aⁿ在aⁿ中，a叫做_______，n叫做______，aⁿ叫做_______;

(2)正数的任何次幂都是______；负数的奇次幂是_______，负数的偶次幂是________;

(3)乘方

(-2)⁵的意义是____________________，结果为________；

(4)-2⁵的意义是____________________，结果为________；

(5)在(-2)⁴中，－2是______，4是______，(-2)⁴读作_______或读作_______.

思路解析：按照乘方定义及幂的结构解题.

答案：(1)乘方　 底数　 指数　 幂

(2)正数　 负数　 正数

(3)5个-2的积　 -32

(4)5个2的积的相反数　 -32

(5)底数　 指数　 负二的四次幂　 负二的四次方

1.5.1　 乘方

5分钟训练(预习类训练，可用于课前)

1.5　 有理数的乘方