
题目列表(包括答案和解析)
1.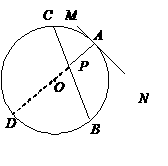 解:如右图,延长AP交⊙O于点D.
解:如右图,延长AP交⊙O于点D.
由相交弦定理,知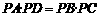 .
.
∵PA=2cm,PB=5cm,PC=3cm,
∴2PD=5×3. ∴PD=7.5.
∴AD=PD+PA=7.5+2=9.5.
∵MN切⊙O于点A,AP⊥MN,
∴AD是⊙O的直径.
∴⊙O的直径是9.5cm.
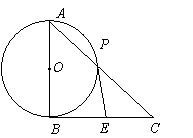
2.如图,AB为⊙O的直径,BC切⊙O于B,AC交⊙O于P,CE=BE,E在BC上. 求证:PE是⊙O的切线.
答案详解:
基础知识: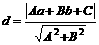 ;
;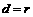 ;公切弦方程.;
;公切弦方程.;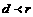 ;
;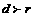 ;
; ;
;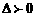 ;
; ;
;
选择题:C;A;D;A;C;B;
填空题:1. 15°; 2. 5; 3. 40
解答题:
1.如图,MN为⊙O的切线,A为切点,过点A作AP⊥MN,交⊙O的弦BC于点P. 若PA=2cm,PB=5cm,PC=3cm,求⊙O的直径.
3.AD、AE和BC分别切⊙O于D、E、F,如果AD=20,则△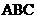 的周长为
的周长为
2. 如图,已知⊙O的直径AB与弦AC的夹角为30°,过C点的切线PC与AB的延长线交于P,PC=5,则⊙O的半径为
如图,已知⊙O的直径AB与弦AC的夹角为30°,过C点的切线PC与AB的延长线交于P,PC=5,则⊙O的半径为
1.A、B、C是⊙O上三点,的度数是50°,∠OBC=40°,则∠OAC等于
6.把直线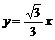 绕原点逆时针方向旋转,使它与圆
绕原点逆时针方向旋转,使它与圆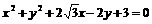 相切,则直线转动的最小正角是( )
相切,则直线转动的最小正角是( )
A.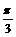 B.
B. 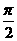 C.
C.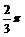 D.
D.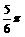
4..设点(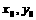 )在圆
)在圆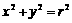 的外部,则直线
的外部,则直线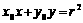 与圆的位置关系是( )
与圆的位置关系是( )
A.相交 B.相切 C. 相离 D.不确定
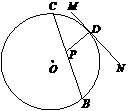
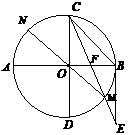
在⊙O中,直径AB、CD互相垂直,BE切⊙O于B,且BE=BC,CE交AB于F,交⊙O于M,连结MO并延长,交⊙O于N,则下列结论中,正确的是( )
A. CF=FM B. OF=FB C. 的度数是22.5° D. BC∥MN
3.给出下列四个命题,其中是真命题的为( )
①角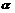 一定是直线
一定是直线 的倾斜角;
的倾斜角;
②点 关于直线
关于直线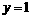 的对称点的坐标是
的对称点的坐标是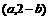 ;
;
③与坐标轴距离相等的点的轨迹方程是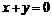 ;
;
④直线 与圆
与圆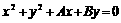 相切.
相切.
A.(1)、(2) B.(3)、(4) C.(1)、(3) D.(2)、(4)
2..倾斜角为60o,且过原点的直线被圆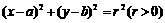 截得的弦长恰等于圆的半径,则
截得的弦长恰等于圆的半径,则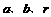 满足的条件是( )
满足的条件是( )
A.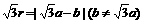 B.
B. 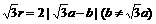
C. 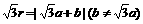 D.
D. 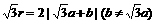
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com