
题目列表(包括答案和解析)
| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(米) | 1.0 | 1.4 | 1.0 | 0.6 | 1.0 | 1.4 | 0.9 | 0.4 | 1.0 |
| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(米) | 1,0 | 1,4 | 1,0 | 0,6 | 1,0 | 1,4 | 0,9 | 0,4 | 1,0 |
某“帆板”集训队在一海滨区域进行集训,该海滨区域的海浪高度![]() (米)随着时间
(米)随着时间![]() 而周期性变化,每天各时刻
而周期性变化,每天各时刻![]() 的浪高数据的平均值如下表:
的浪高数据的平均值如下表:
|
| 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
|
| 1.0 | 1.4 | 1.0 | 0.6 | 1.0 | 1.4 | 0.9 | 0.5 | 1.0 |
试画出散点图;
观察散点图,从![]() 中选择一个合适的函数模型,并求出该拟合模型的解析式;
中选择一个合适的函数模型,并求出该拟合模型的解析式;
如果确定在白天7时~19时当浪高不低于0.8米时才进行训练,试安排恰当的训练时间.
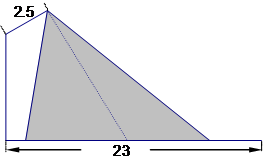 在路边安装路灯,路宽23m,灯杆长2.5m,且与灯柱成120°角.路灯采用锥形灯罩,灯罩轴线与灯杆垂直.当灯柱高h为多少米时,灯罩轴线正好通过道路路面的中线?(精确到0.01m)(
在路边安装路灯,路宽23m,灯杆长2.5m,且与灯柱成120°角.路灯采用锥形灯罩,灯罩轴线与灯杆垂直.当灯柱高h为多少米时,灯罩轴线正好通过道路路面的中线?(精确到0.01m)(| 3 |
在边长为4的正方形ABCD的边上有一点P沿着折线BCDA由点B(起点)向点A(终点)运动.设点P运动的路程为x, 的面积为y,且y与x之间的函数关系式用如图所示的程序框图给出.
的面积为y,且y与x之间的函数关系式用如图所示的程序框图给出.
(1)写出框图中①、②、③处应填充的式子;(2)若输出的面积y值为6,则路程x的值为多少?并指出此时点P的在正方形的什么位置上?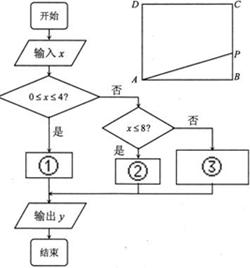
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com