
题目列表(包括答案和解析)
(14分)已知圆 过点
过点 且与圆M:
且与圆M: 关于直线
关于直线 对称
对称
(1)判断圆 与圆M的位置关系,并说明理由;
与圆M的位置关系,并说明理由;
(2)过点 作两条相异直线分别与圆
作两条相异直线分别与圆 相交于
相交于 、
、
①若直线 与直线
与直线 互相垂直,求
互相垂直,求 的最大值;
的最大值;
②若直线 与直线
与直线 与
与 轴分别交于
轴分别交于 、
、 ,且
,且 ,
, 为坐标原点,试判断直线
为坐标原点,试判断直线 与
与 是否平行?请说明理由.
是否平行?请说明理由.
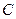 过点
过点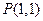 且与圆M:
且与圆M: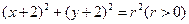 关于直线
关于直线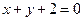 对称
对称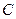 与圆M的位置关系,并说明理由;
与圆M的位置关系,并说明理由;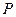 作两条相异直线分别与圆
作两条相异直线分别与圆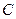 相交于
相交于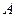 、
、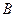
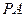 与直线
与直线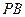 互相垂直,求
互相垂直,求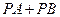 的最大值;
的最大值;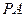 与直线
与直线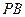 与
与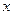 轴分别交于
轴分别交于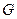 、
、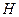 ,且
,且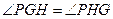 ,
,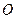 为坐标原点,试判断直线
为坐标原点,试判断直线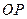 与
与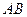 是否平行?请说明理由.
是否平行?请说明理由.| 3 |
| 3 |
| 2 |
| 2 |
(12分)已知圆 关于直线
关于直线 对称,圆心在第二象限,半径为
对称,圆心在第二象限,半径为 。
。
⑴求圆C的方程;
⑵已知不过原点的直线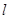 与圆C相切,且
与圆C相切,且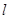 在
在 轴、
轴、 轴上的截距相等,求直线
轴上的截距相等,求直线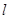 的方程。
的方程。
一、选择题:
1.C 2.D 3.C 4.D 5.C 6.A 7.A 8.D 9.D 10.B
二、填空题:
11. .files/image346.gif) 12.
12. .files/image348.gif) 13.
13. .files/image350.gif) 14.7 15.
14.7 15. .files/image352.gif) 16.
16. .files/image354.gif) 17.
17. .files/image356.gif)
18. 答案不惟一,如.files/image358.gif) ,或
,或.files/image360.gif) 等 19. 60 20.
等 19. 60 20. .files/image362.gif) 21.
21. .files/image364.gif)
22. .files/image366.gif) 23.
23. .files/image368.gif) 24.
24. .files/image370.gif)
三、解答题:
25 解: (Ⅰ)因为.files/image214.gif) ,∴
,∴.files/image373.gif) ,则
,则.files/image375.gif)
∴.files/image377.gif)
(Ⅱ)由.files/image222.gif) ,得
,得.files/image380.gif) ,∴
,∴.files/image382.gif)
则.files/image384.gif)
由正弦定理,得.files/image386.gif) ,∴
,∴.files/image077.gif) 的面积为
的面积为.files/image388.gif)
26解:(Ⅰ)因为.files/image247.gif) ,
,.files/image390.gif) ,且
,且.files/image392.gif) ,
,
所以.files/image394.gif)
又.files/image238.gif) ,所以四边形
,所以四边形.files/image396.gif) 为平行四边形,则
为平行四边形,则.files/image398.gif)
而.files/image242.gif) ,故点
,故点.files/image075.gif) 的位置满足
的位置满足.files/image400.gif)
(Ⅱ)证: 因为侧面.files/image231.gif) 底面
底面.files/image233.gif) ,
,.files/image402.gif) ,且
,且.files/image404.gif) ,
,
所以.files/image406.gif) ,则
,则.files/image408.gif)
又.files/image235.gif) ,且
,且.files/image410.gif) ,所以
,所以.files/image412.gif)
而.files/image414.gif) ,所以
,所以.files/image249.gif)
27解:(Ⅰ)因为.files/image416.gif) ,所以
,所以.files/image254.gif) 的面积为
的面积为.files/image418.gif) (
(.files/image420.gif) )
)
设正方形.files/image264.gif) 的边长为
的边长为.files/image315.gif) ,则由
,则由.files/image423.gif) ,得
,得.files/image425.gif) ,
,
解得.files/image427.gif) ,则
,则.files/image429.gif)
所以.files/image431.gif) ,则
,则.files/image433.gif)
(Ⅱ)因为.files/image435.gif) ,所以
,所以.files/image437.gif)
.files/image439.gif)
当且仅当.files/image441.gif) 时取等号,此时
时取等号,此时.files/image443.gif) .所以当
.所以当.files/image277.gif) 长为
长为.files/image446.gif) 时,
时,.files/image133.gif) 有最小值1
有最小值1
28解:(Ⅰ)设圆心.files/image279.gif)
.files/image448.gif) ,则
,则.files/image450.gif) ,解得
,解得.files/image452.gif)
则圆.files/image279.gif) 的方程为
的方程为.files/image454.gif) ,将点
,将点.files/image295.gif) 的坐标代入得
的坐标代入得.files/image457.gif) ,故圆
,故圆.files/image279.gif) 的方程为
的方程为.files/image459.gif)
(Ⅱ)设.files/image461.gif) ,则
,则.files/image459.gif) ,且
,且.files/image463.gif)
=.files/image465.gif) =
=.files/image467.gif) ,
,
所以.files/image293.gif) 的最小值为
的最小值为.files/image469.gif) (可由线性规划或三角代换求得)
(可由线性规划或三角代换求得)
(Ⅲ)由题意知, 直线.files/image299.gif) 和直线
和直线.files/image301.gif) 的斜率存在,且互为相反数,故可设
的斜率存在,且互为相反数,故可设.files/image471.gif) ,
,
.files/image473.gif) ,由
,由.files/image475.gif) ,
,
得.files/image477.gif)
因为点.files/image295.gif) 的横坐标
的横坐标.files/image480.gif) 一定是该方程的解,故可得
一定是该方程的解,故可得.files/image482.gif)
同理,.files/image484.gif) ,
,
所以.files/image486.gif) =
=.files/image488.gif)
所以,直线.files/image256.gif) 和
和.files/image304.gif) 一定平行
一定平行
29解:(Ⅰ)因为.files/image490.gif)
由.files/image492.gif) ;由
;由.files/image494.gif) ,
,
所以.files/image317.gif) 在
在.files/image497.gif) 上递增,在
上递增,在.files/image499.gif) 上递减
上递减
欲.files/image317.gif) 在
在.files/image309.gif) 上为单调函数,则
上为单调函数,则.files/image501.gif)
(Ⅱ)证:因为.files/image317.gif) 在
在.files/image497.gif) 上递增,在
上递增,在.files/image499.gif) 上递减,
上递减,
所以.files/image317.gif) 在
在.files/image480.gif) 处取得极小值
处取得极小值.files/image504.gif)
又.files/image506.gif) ,所以
,所以.files/image317.gif) 在
在.files/image508.gif) 上的最小值为
上的最小值为.files/image510.gif)
从而当.files/image311.gif) 时,
时,.files/image513.gif) ,即
,即.files/image515.gif)
(Ⅲ)证:因为.files/image517.gif) ,所以
,所以.files/image325.gif) 即为
即为.files/image519.gif) ,
,
令.files/image521.gif) ,从而问题转化为证明方程
,从而问题转化为证明方程.files/image521.gif) =0
=0
在.files/image523.gif) 上有解,并讨论解的个数
上有解,并讨论解的个数
因为www.tesoon.com.files/image525.gif) ,
,.files/image527.gif) ,
,
所以 ①当.files/image529.gif) 时,
时,.files/image531.gif) ,
,
所以.files/image533.gif) 在
在.files/image523.gif) 上有解,且只有一解
上有解,且只有一解
②当.files/image536.gif) 时,
时,.files/image538.gif) ,但由于
,但由于.files/image540.gif) ,
,
所以.files/image533.gif) 在
在.files/image523.gif) 上有解,且有两解
上有解,且有两解
③当.files/image543.gif) 时,
时,.files/image545.gif) ,所以
,所以.files/image533.gif) 在
在.files/image523.gif) 上有且只有一解;
上有且只有一解;
当.files/image548.gif) 时,
时,.files/image550.gif) ,
,
所以.files/image533.gif) 在
在.files/image552.gif) 上也有且只有一解
上也有且只有一解
综上所述, 对于任意的.files/image321.gif) ,总存在
,总存在.files/image323.gif) ,满足
,满足.files/image325.gif) ,
,
且当.files/image554.gif) 时,有唯一的
时,有唯一的.files/image556.gif) 适合题意;
适合题意;
当.files/image536.gif) 时,有两个
时,有两个.files/image556.gif) 适合题意
适合题意
30解:(Ⅰ)由题意得,.files/image558.gif) ,所以
,所以.files/image333.gif) =
=.files/image561.gif)
(Ⅱ)证:令.files/image563.gif) ,
,.files/image565.gif) ,则
,则.files/image337.gif) =1
=1
所以.files/image331.gif) =
=.files/image567.gif) (1),
(1),.files/image569.gif) =
=.files/image571.gif) (2),
(2),
(2)―(1),得.files/image573.gif) ―
―.files/image575.gif) =
=.files/image577.gif) ,
,
化简得.files/image579.gif) (3)
(3)
.files/image581.gif) (4),(4)―(3)得
(4),(4)―(3)得.files/image583.gif)
在(3)中令.files/image563.gif) ,得
,得.files/image585.gif) ,从而
,从而.files/image329.gif) 为等差数列
为等差数列
(Ⅲ)记.files/image587.gif) ,公差为
,公差为.files/image589.gif) ,则
,则.files/image344.gif) =
=.files/image591.gif)
则.files/image593.gif) ,
,.files/image595.gif)
.files/image597.gif)
.files/image599.gif)
则.files/image601.gif) ,当且仅当
,当且仅当.files/image603.gif) ,即
,即.files/image605.gif) 时等号成立
时等号成立
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com