(本小题满分12分) 某食品企业一个月内被消费者投诉的次数用表示，.   

椐统计，随机变量的概率分布如下：

(Ⅰ)求a的值和的数学期望；

（Ⅱ）假设一月份与二月份被消费者投诉的次数互不影响,求该企业在这两个月内共被消费者投诉2次的概率。

(本小题满分12分)某投资商到一开发区投资72万元建起一座蔬菜加工厂，第一年共支出12万元，以后每年支出增加4万元，从第一年起每年蔬菜销售收入为50万元.设表示前年的纯利润总和, 表示前年的总支出.

[前年的总收入-前年的总支出-投资额].

（1）写出的关系式

(2) 写出前年的纯利润总和关于的函数关系式；并求该厂从第几年开始盈利?

(3)若干年后,投资商为开发新项目,对该厂有两种处理方案:①年平均纯利润达到最大时,以48万元出售该厂；②纯利润总和达到最大时，以16万元万元出售该厂，问哪种方案更合算？

(本小题满分12分)某商场销售某种商品的经验表明，该商品每日的销售量（单位：千克）与销售价格（单位：元/千克）满足关系式，其中，为常数，已知销售价格为5元/千克时，每日可售出该商品11千克。

（1）求的值；

（2）若该商品的成本为3元/千克，试确定销售价格的值，使商场每日销售该商品所获得的利润最大。

(本小题满分12分)

某工厂生产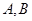两种元件，其质量按测试指标划分为：大于或等于7．5为正品，小于7．5为次品．现从一批产品中随机抽取这两种元件各5件进行检测，检测结果记录如下：

   由于表格被污损，数据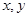看不清，统计员只记得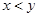，且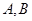两种元件的检测数据的平均值相等，方差也相等．

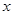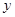（Ⅰ）求表格中与的值；

（Ⅱ）若从被检测的5件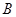种元件中任取2件，求2件都为正品的概率．

(本小题满分12分)某企业准备招聘一批大学生到本单位就业，但在签约前要对他们的某项专业技能进行测试．在待测试的某一个小组中有男、女生共10人（其中女生人数多于男生人数），如果从中随机选2人参加测试，其中恰为一男一女的概率为；（Ⅰ）求该小组中女生的人数；（Ⅱ）假设此项专业技能测试对该小组的学生而言，每个女生通过的概率均为，每个男生通过的概率均为；现对该小组中男生甲、男生乙和女生丙3个人进行测试，记这3人中通过测试的人数为随机变量，求的分布列和数学期望.