
题目列表(包括答案和解析)
7. ![]() 解析:因为f(x)=3ax+1-2a在(0,1)上存在
解析:因为f(x)=3ax+1-2a在(0,1)上存在![]() 使
使![]() ,所以f(0)f(1)<0,即(1-2a)(a+1)<0所以
,所以f(0)f(1)<0,即(1-2a)(a+1)<0所以![]()
已知随机变量Y的所有可能取值为1,2,…,n,且取这些值的概率依次为k,2k,…,nk,求常数k的值.
已知曲线C: (m∈R)
(m∈R)
(1) 若曲线C是焦点在x轴点上的椭圆,求m的取值范围;
(2) 设m=4,曲线c与y轴的交点为A,B(点A位于点B的上方),直线y=kx+4与曲线c交于不同的两点M、N,直线y=1与直线BM交于点G.求证:A,G,N三点共线。
【解析】(1)曲线C是焦点在x轴上的椭圆,当且仅当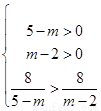 解得
解得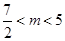 ,所以m的取值范围是
,所以m的取值范围是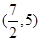
(2)当m=4时,曲线C的方程为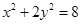 ,点A,B的坐标分别为
,点A,B的坐标分别为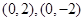 ,
,
由 ,得
,得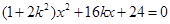
因为直线与曲线C交于不同的两点,所以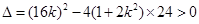
即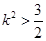
设点M,N的坐标分别为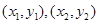 ,则
,则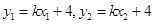
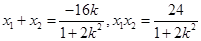
直线BM的方程为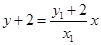 ,点G的坐标为
,点G的坐标为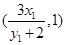
因为直线AN和直线AG的斜率分别为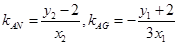
所以
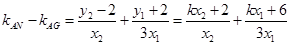
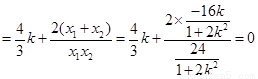
即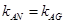 ,故A,G,N三点共线。
,故A,G,N三点共线。
已知函数
 的图像上两相邻最高点的坐标分别为
的图像上两相邻最高点的坐标分别为 和
和 .(Ⅰ)求
.(Ⅰ)求 与
与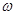 的值;(Ⅱ)在
的值;(Ⅱ)在 中,
中, 分别是角
分别是角 的对边,且
的对边,且 求
求 的取值范围.
的取值范围.
【解析】本试题主要考查了三角函数的图像与性质的综合运用。
第一问中,利用 所以由题意知:
所以由题意知: ,
, ;第二问中,
;第二问中, ,即
,即 ,又
,又 ,
,
则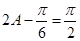 ,解得
,解得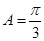 ,
,
所以
结合正弦定理和三角函数值域得到。
解:(Ⅰ) ,
,
所以由题意知: ,
, ;
;
(Ⅱ) ,即
,即 ,又
,又 ,
,
则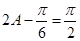 ,解得
,解得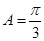 ,
,
所以
因为 ,所以
,所以 ,所以
,所以
你以前听说过“鸡兔同笼”问题吗?这个问题,是我国古代著名趣题之一.大约在1 500年前,《孙子算经》中就记载了这个有趣的问题.书中是这样叙述的:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”这四句话的意思是:有若干只鸡兔同在一个笼子里,从上面数,有35个头;从下面数,有94只脚.求笼中各有几只鸡和兔?
你会解答这个问题吗?你想知道《孙子算经》中是如何解答这个问题的吗?
解答思路是这样的:假如砍去每只鸡、每只兔一半的脚,则每只鸡就变成了“独角鸡”,每只兔就变成了“双脚兔”.这样,(1)鸡和兔的脚的总数就由94只变成了47只;(2)如果笼子里有一只兔子,则脚的总数就比头的总数多1.因此,脚的总只数47与总头数35的差,就是兔子的只数,即47-35=12(只).显然,鸡的只数就是35-12=23(只)了.
这一思路新颖而奇特,其“砍足法”也令古今中外数学家赞叹不已.这种思维方法叫化归法.
化归法就是在解决问题时,先不对问题采取直接的分析,而是将题中的条件或问题进行变形,使之转化,直到最终把它归成某个已经解决的问题.
1.古代《孙子算经》就有这么好的解法——化归法,这一思路新颖而奇特,其“砍足法”也令古今中外数学家赞叹不已.对此,谈谈你的看法.
2.我国古代数学研究一直处于领先地位,现在有所落后了,对此,我们不应只感叹古人的伟大,而更应该树立为科学而奋斗终身的信心,同学们,你们准备好了吗?
设函数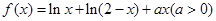 .
.
(Ⅰ) 当 时,求
时,求 的单调区间;
的单调区间;
(Ⅱ) 若 在
在 上的最大值为
上的最大值为 ,求
,求 的值.
的值.
【解析】第一问中利用函数 的定义域为(0,2),
的定义域为(0,2), .
.
当a=1时, 所以
所以 的单调递增区间为(0,
的单调递增区间为(0, ),单调递减区间为(
),单调递减区间为( ,2);
,2);
第二问中,利用当 时,
时, >0, 即
>0, 即 在
在 上单调递增,故
上单调递增,故 在
在 上的最大值为f(1)=a 因此a=1/2.
上的最大值为f(1)=a 因此a=1/2.
解:函数 的定义域为(0,2),
的定义域为(0,2), .
.
(1)当 时,
时, 所以
所以 的单调递增区间为(0,
的单调递增区间为(0, ),单调递减区间为(
),单调递减区间为( ,2);
,2);
(2)当 时,
时, >0, 即
>0, 即 在
在 上单调递增,故
上单调递增,故 在
在 上的最大值为f(1)=a 因此a=1/2.
上的最大值为f(1)=a 因此a=1/2.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com