
题目列表(包括答案和解析)
已知函数 的最小值为0,其中
的最小值为0,其中
(Ⅰ)求 的值;
的值;
(Ⅱ)若对任意的 有
有 ≤
≤ 成立,求实数
成立,求实数 的最小值;
的最小值;
(Ⅲ)证明 (
( ).
).
【解析】(1)解:
 的定义域为
的定义域为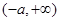

由 ,得
,得
当x变化时, ,
, 的变化情况如下表:
的变化情况如下表:
|
x |
|
|
|
|
|
- |
0 |
+ |
|
|
|
极小值 |
|
因此, 在
在 处取得最小值,故由题意
处取得最小值,故由题意 ,所以
,所以
(2)解:当 时,取
时,取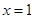 ,有
,有 ,故
,故 时不合题意.当
时不合题意.当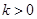 时,令
时,令 ,即
,即

令 ,得
,得
①当 时,
时, ,
, 在
在 上恒成立。因此
上恒成立。因此 在
在 上单调递减.从而对于任意的
上单调递减.从而对于任意的 ,总有
,总有 ,即
,即 在
在 上恒成立,故
上恒成立,故 符合题意.
符合题意.
②当 时,
时, ,对于
,对于 ,
, ,故
,故 在
在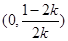 上单调递增.因此当取
上单调递增.因此当取 时,
时, ,即
,即 不成立.
不成立.
故 不合题意.
不合题意.
综上,k的最小值为 .
.
(3)证明:当n=1时,不等式左边= =右边,所以不等式成立.
=右边,所以不等式成立.
当 时,
时,


在(2)中取 ,得
,得
 ,
,
从而

所以有





综上,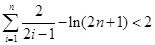 ,
,
已知函数![]() 的最小值为
的最小值为![]()
(Ⅰ)求![]()
(Ⅱ)是否存在实数m,n同时满足下列条件:
①m>n>3;
②当![]() 的定义域为[n,m]时,值域为[n2,m2]?
的定义域为[n,m]时,值域为[n2,m2]?
若存在,求出m,n的值;若不存在,说明理由.
已知函数![]() 的最小值为
的最小值为![]()
(Ⅰ)求![]()
(Ⅱ)是否存在实数m,n同时满足下列条件:
① m>n>3;
② ②当![]() 的定义域为[n,m]时,值域为[n2,m2]?
的定义域为[n,m]时,值域为[n2,m2]?
若存在,求出m,n的值;若不存在,说明理由.
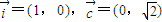 ,若过定点
,若过定点 、以
、以 (λ∈R)为法向量的直线l1与过点
(λ∈R)为法向量的直线l1与过点 以
以 为法向量的直线l2相交于动点P.
为法向量的直线l2相交于动点P. 恒为定值;
恒为定值; 上的两个动点,且
上的两个动点,且 ,试问当|MN|取最小值时,向量
,试问当|MN|取最小值时,向量 与
与 是否平行,并说明理由.
是否平行,并说明理由.已知函数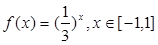 ,函数
,函数 的最小值为
的最小值为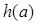 。
。
(1)求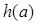 的表达式。
的表达式。
(2)是否存在实数m,n同时满足以下条件:
① m>n>3;
② 当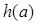 的定义域为[m,n]时,值域为
的定义域为[m,n]时,值域为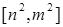
若存在,求出m,n的值;若不存在,说明理由。
一、选择题:
1.A 2.B 3.A 4.D 5.B
6.A 7.A 8.B 9.C 10.B
二、填空题:
11.{2,3} 12..files/image260.gif) 13.1+i 14.3 15.
13.1+i 14.3 15..files/image262.gif) 16.24 17.
16.24 17..files/image264.gif) 18.
18..files/image266.gif) 19.2 20.
19.2 20..files/image268.gif) 21. 45 22.
21. 45 22..files/image270.gif) 23.2 24.
23.2 24..files/image272.gif)
三、解答题:
25解:(1)原式展开得:.files/image274.gif)
.files/image276.gif)
.files/image278.gif)
.files/image280.gif)
(2).files/image282.gif)
26解:(1)设事件.files/image224.gif) 为A,则在7次抛骰子中出现5次奇数,2次偶数
为A,则在7次抛骰子中出现5次奇数,2次偶数
而抛骰子出现的奇数和偶数的概率为P是相等的,且为.files/image285.gif)
根据独立重复试验概率公式:.files/image287.gif)
(2)若.files/image289.gif)
即前2次抛骰子中都是奇数或都是偶数.
若前2次都是奇数,则必须在后5次中抛出3次奇数2次偶数,
其概率:.files/image291.gif)
若前2次都是偶数,则必须在后5次中抛出5次奇数,其概率:
.files/image293.gif)
.files/image295.gif) 所求事件的概率
所求事件的概率.files/image297.gif)
27解:(1)由题得.files/image299.gif)
.files/image301.gif)
设.files/image303.gif)
.files/image305.gif)
两式相减:.files/image307.gif)
.files/image309.gif)
.files/image311.gif)
(2).files/image313.gif)
.files/image315.gif)
.files/image317.gif)
.files/image319.gif) ,即取
,即取.files/image321.gif) 时,
时,.files/image323.gif) .
.
所求的最小自然数是15
28解:(1)正方体ABCD中,∵A.N分别是AD.BC的中点,∴MN⊥AD
又∵PA⊥平面α,MN.files/image325.gif) α,∴PA⊥MN,∴MN⊥平面PAD
α,∴PA⊥MN,∴MN⊥平面PAD
又MN.files/image325.gif) 平面PAD,平面PMN⊥平面PAD
平面PAD,平面PMN⊥平面PAD
(2)由上可知:MN⊥平面PAD
∴PM⊥MN,QM⊥MN,∠PMQ是二面角P―MN―Q的平面角
PA=2,AD=2,则AM=1,PM=.files/image328.gif)
PD=2.files/image330.gif) ,MQ=
,MQ=.files/image332.gif)
.files/image334.gif)
29解:(1)抛物线的焦点是(.files/image336.gif) ),则双曲线的
),则双曲线的.files/image338.gif)
设双曲线方程:.files/image340.gif)
解得:.files/image342.gif)
(2)联立方程:.files/image344.gif)
当.files/image346.gif)
由韦达定理:.files/image348.gif)
设.files/image350.gif)
.files/image352.gif) 代入可得:
代入可得:.files/image354.gif) ,检验合格
,检验合格
30解:(1).files/image356.gif) ,
,
.files/image358.gif)
(2)令.files/image360.gif) ,
,
在[-1,3]中,.files/image362.gif) 在此区间为增函数
在此区间为增函数.files/image364.gif) 时,
时,
.files/image366.gif) 在此区间为减函数.
在此区间为减函数.
.files/image368.gif)
.files/image370.gif) 处取得极大值
处取得极大值
.files/image372.gif) [
[.files/image370.gif) ,3]时
,3]时.files/image374.gif) 在此区间为增函数,
在此区间为增函数,.files/image376.gif) 在x=3处取得极大值.
在x=3处取得极大值.
比较.files/image378.gif) (-
(-.files/image370.gif) )和
)和.files/image380.gif) 的大小得:
的大小得:.files/image382.gif)
(无理由.files/image380.gif) 最大,扣3分)
最大,扣3分)
.files/image384.gif) 即存在k=2007
即存在k=2007
(3).files/image386.gif)
.files/image388.gif)
而.files/image390.gif)
(也可由单调性:.files/image392.gif)
.files/image394.gif)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com