练习册

  • 练习册
  • 试题
    A p>0 ,q=0 B p<0 ,q=0 C p≤0.q＝0 D p≥0.q=0 【查看更多】

     

    题目列表(包括答案和解析)

    已知命题p：A={x||x-a|＜4}，命题q：B={x|（x-2）（3-x）＞0}，若p是q的必要条件，则实数a的取值范围是
    [-1，6]
    [-1，6]
    ．

    查看答案和解析>>

    当a，b，c∈(0，＋∞)时，由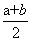≥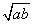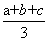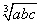，≥，运用归纳推理，可猜测出的合理结论是(　　)

    A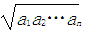．≥ (ai>0，i＝1,2，…n)

    B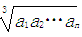．≥ (ai>0，i＝1,2，…n)

    C．≥ (ai∈R，i＝1,2，…n)

    D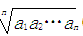．≥ (ai>0，i＝1,2，…n)

     

    查看答案和解析>>

    已知0<a<b，且a＋b＝1，则下列不等式中，正确的是(　　)

    A．log2a>0                              B．2a－b<

    C．2<                             D．log2a＋log2b<－2

    查看答案和解析>>

    已知F1(-4,0)、F2(4,0),曲线上动点P到F1、F2的距离之差为6,则曲线的方程为(    )

    A.-=1(x>0)                       B.-=1

    C.-=1(y>0)                       D.-=1

    查看答案和解析>>

    已知f(x)＝x3＋x，若a，b，c∈R，且a＋b>0，a＋c>0，b＋c>0，则f(a)＋f(b)＋f(c)的值(　 　)

    A．一定大于0        B．一定等于0        C．一定小于0        D．正负都有可能

     

    查看答案和解析>>

    一、选择题：(本大题共10小题,每小题5分,共50分)

      1　B  2　A  3　 文C（理C） 4　 D  5　 文A（理B） 6　 文B（理C）   7　 文C（理C）   8　 文C（理A）   9　 文A （理D） 10　 文D（理A）

    二、填空题：（本大题共6小题，每小题4分，共24分　）

    11　 （文）“若，则” ，（理）

    12　 （文） ，（理）， 

    13　 （文），（理）－2

    14　 -2      15　           16　 ②④

    三、解答题：（本大题共6个解答题，满分76分，）

    17　 （文）解：以AN所在直线为x轴，AN的中垂

    线为y轴建立平面直角坐标系如图所示，

    则A(-4,0),N(4,0),设P（x，y）  

    由|PM|：|PN|=，|PM|2=|PA|2 ?|MA|2得：

                                 

    代入坐标得：        

    整理得：                        

    即                            

    所以动点P的轨迹是以点

    （理）解：(I)当a=1时  

                                

     或或         

     或                              

    (II)原不等式              

    设有 

    当且仅当

    即时                    

    依题有：10a<10  ∴为所求　 

     18　 （文）解：

      

       解得        

                       

                                

     

    若由方程组解得，可参考给分

    （理）解：(Ⅰ)设    （a≠0），则

               ……     ①

              ……    ②

    又∵有两等根

          ∴……  ③

    由①②③得                         

    又∵

      ∴a<0, 故

    ∴                        

        (Ⅱ)

                            

           ∵g(x)无极值

           ∴方程

          

          得                      

    19　 （文）解：(I)当a=1时  

                                

     或或         

     或                             

    (II)原不等式              

    设有 

    当且仅当

    即时                   

    依题有：10a<10  ∴为所求　                      

     

    （理）解：以AN所在直线为x轴，AN的中垂

    线为y轴建立平面直角坐标系如图所示，

    则A(-4,0),N(4,0),设P（x，y）  

    由|PM|：|PN|=，|PM|2=|PA|2 ?|MA|2得：

                                  

    代入坐标得：        

    整理得：                       

    即                            

    所以动点P的轨迹是以点

    20　 （文）解：(Ⅰ)设    （a≠0），则

               ……     ①

              ……    ②

    又∵有两等根

          ∴……  ③

    由①②③得                         

    又∵

      ∴a<0, 故

    ∴                       

        (Ⅱ)

                            

           ∵g(x)无极值

           ∴方程

          

          得                             

    （理）解：（I）设       （1）

    又故     （2）

    由（1），（2）解得              

    （II）由向量与向量的夹角为得

    由及A+B+C=知A+C=

    则            

         

    由0<A<得，得

    故的取值范围是                      

     

    21　 　解：（I）由已知得Sn=2an-3n，

    Sn+1=2an+1-3(n+1),两式相减并整理得：an+1=2an+3            

    所以3+ an+1=2（3+an），又a1=S1=2a1-3，a1=3可知3+ a1=6，进而可知an+3

    所以，故数列{3+an}是首相为6，公比为2的等比数列，

    所以3+an=6,即an=3()                           

    同步练习册答案