
题目列表(包括答案和解析)
(本题满分6分)
先化简,再求值: ,其中x=-5.
,其中x=-5.
(本题满分6分)
先化简,再求值: ,其中x=-5.
,其中x=-5.
 ,如果存在给定的实数对(
,如果存在给定的实数对( ),使得
),使得 恒成立,则称
恒成立,则称 为“S-函数”.
为“S-函数”. 是否是“S-函数”;
是否是“S-函数”; 是一个“S-函数”,求出所有满足条件的有序实数对
是一个“S-函数”,求出所有满足条件的有序实数对 ;
;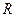 的函数
的函数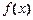 是“S-函数”,且存在满足条件的有序实数对
是“S-函数”,且存在满足条件的有序实数对 和
和 ,当
,当 时,
时, 的值域为
的值域为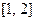 ,求当
,求当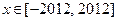 时函数
时函数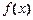 的值域.
的值域.(本题 满分14分,第(1)小题4分,第(2)小题①6分、第(2)小题②4分)
满分14分,第(1)小题4分,第(2)小题①6分、第(2)小题②4分)
直角三角板ABC中,∠A=30°,BC=1.将其绕直角顶点C逆时针旋转一个角 (
( 且
且 ≠ 90°),得到Rt△
≠ 90°),得到Rt△ ,
,
(1)如图9,当 边经过点B时,求旋转角
边经过点B时,求旋转角 的度数;
的度数;
(2)在三角板旋转的过程中,边 与AB所在直线交于点D,过点 D作DE∥
与AB所在直线交于点D,过点 D作DE∥ 交
交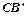 边于点E,联结BE.
边于点E,联结BE.
①当 时,设
时,设 ,
,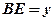 ,求
,求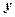 与
与 之间的函数解析式及定义域;
之间的函数解析式及定义域;
②当 时,求
时,求 的长.
的长. 

(本题满分12分,第(1)小题满分6分,第(2)小题满分6分)如图7,等腰三角形ABC中,AB=AC,AH垂直BC,点E是AH上一点,延长AH至点F,使FH=EH,
(1)求证:四边形EBFC是菱形;
(2)如果![]() =
=![]() ,求证:
,求证:![]() .
.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com