
题目列表(包括答案和解析)
(本小题满分12分)
古代印度婆罗门教寺庙内的僧侣们曾经玩过一种被称为“河内宝塔问题”的游戏,其玩法如下:如图,设有n(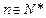 )个圆盘依其半径大小,大的在下,小的在上套在A柱上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子A、B、C可供使用.
)个圆盘依其半径大小,大的在下,小的在上套在A柱上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子A、B、C可供使用.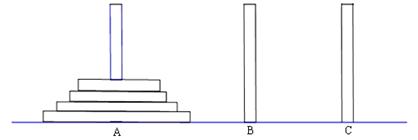
现用an表示将n个圆盘全部从A柱上移到C柱上所至少需要移动的次数,回答下列问题:
(1) 写出a1,a2,a3,并求出an;
(2) 记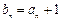 ,求和
,求和 (
( );
);
(其中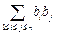 表示所有的积
表示所有的积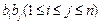 的和)
的和)
(3) 证明: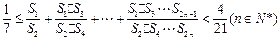 .
.
(本小题满分12分)已知函数f(x)=x3+x2-2.
(1)设{an}是正数组成的数列,前n项和为Sn,其中a1=3.若点(an,an+12-2an+1)(n∈N*)在函数y=f′(x)的图象上,求证:点(n,Sn)也在y=f′(x)的图象上;
(2)求函数f(x)在区间(a-1,a)内的极值.
1. (本小题满分12分)
古代印度婆罗门教寺庙内的僧侣们曾经玩过一种被称为“河内宝塔问题”的游戏,其玩法如下:如图,设有n( )个圆盘依其半径大小,大的在下,小的在上套在A柱上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子A、B、C可供使用.
)个圆盘依其半径大小,大的在下,小的在上套在A柱上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子A、B、C可供使用.

现用an表示将n个圆盘全部从A柱上移到C柱上所至少需要移动的次数,回答下列问题:
(1) 写出a1,a2,a3,并求出an;
(2) 记 ,求和
,求和 (
( );
);
(其中 表示所有的积
表示所有的积 的和)
的和)
(3) 证明: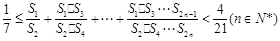 .
.
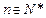 )个圆盘依其半径大小,大的在下,小的在上套在A柱上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子A、B、C可供使用.
)个圆盘依其半径大小,大的在下,小的在上套在A柱上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子A、B、C可供使用.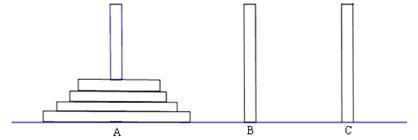
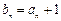 ,求和
,求和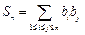 (
(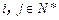 );
); 表示所有的积
表示所有的积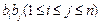 的和)
的和)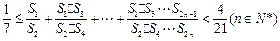 .
.一、选择题(本大题12小题,每小题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
C
D
D
A
B
C
C
C
A
D
A
二、填空题(本大题共4小题,每小题4分,共16分)
13.4949; 14.[.files\image083.gif) ] 15.②④; 16.x<0或x>2
] 15.②④; 16.x<0或x>2
三、解答题(本大题共6小题共74分)
17.解(1)设.files\image085.gif) ,由
,由.files\image087.gif) ,有x+y=-1 ①……………1分
,有x+y=-1 ①……………1分
.files\image027.gif) 与
与.files\image056.gif) 的夹角为
的夹角为.files\image059.gif) ,有
,有.files\image092.gif) ,
,
∴.files\image094.gif) ,则x2+y2=1 ②……………2分
,则x2+y2=1 ②……………2分
由①②解得.files\image096.gif) ,∴
,∴.files\image098.gif) (-1,0)或
(-1,0)或.files\image098.gif) (0,-1) ……………4分
(0,-1) ……………4分
(2)由2B=A+C知B=.files\image101.gif) ……………5分
……………5分
由.files\image103.gif) 垂直知
垂直知.files\image098.gif) (0,-1),则
(0,-1),则
.files\image105.gif) ……………6分
……………6分
∴.files\image107.gif)
=1+.files\image109.gif) ……………8分
……………8分
∵0<A<.files\image111.gif)
∴-1≤cos(2A+.files\image113.gif) )<
)<.files\image115.gif)
即.files\image117.gif) ………………10分
………………10分
故.files\image119.gif) ………………12分
………………12分
18.解:(1)过点A作AF⊥CB交CB延长线于点F,连结EF,则AF⊥平面BCC1B1,∠AEF为所求直线AE与平面BCC1B1所成的角. …………………2分
在Rt△AEF中,AF=.files\image121.gif) ∠AEF=
∠AEF=.files\image123.gif)
故直线AE与平面BCC1B1所成的角为arctan.files\image125.gif) …………………6分
…………………6分
(2)以O为原点,OB为x轴,OC为y轴,建立空间直角坐标系O-xyz,则
A (0,-.files\image127.gif) ),E (0,
),E (0,.files\image129.gif) ),D1 (-1,0,2)
),D1 (-1,0,2)
.files\image131.gif) …………………8分
…………………8分
设平面AED1的一个法向量.files\image133.gif) 则
则
.files\image135.gif) 取z=2
取z=2.files\image002.gif) ,得
,得.files\image056.gif) =(3
=(3.files\image002.gif) ,-1,2
,-1,2.files\image002.gif) )
)
∴点O到平面AED1的距离为d=.files\image140.gif) …………………12分
…………………12分
19.解(1)由(an+1+an+2+an+3)-(an+an+1+an+2)=1.files\image142.gif) ,
,
∴a1?a4,a7…,a3n-2是首项为1,公差为1的等差数列,
∴Pn=.files\image144.gif) …………………4分
…………………4分
由.files\image146.gif)
∴b2,b5,b8, …b3n-1是以1为首项,公比为-1的等比数列
∴Qn=.files\image148.gif) …………………8分
…………………8分
(2)对于Pn≤100Qn
当n为偶数时,不等式显然不成立;
当n为奇数时,.files\image150.gif) ,解得n=1,3,…,13.
,解得n=1,3,…,13.
所求之和为.files\image152.gif) ………………12分
………………12分
20.解∵P(x=6)=.files\image154.gif) ………………3分
………………3分
P(x=7)=.files\image156.gif) ………………6分
………………6分
P(x=8)=.files\image158.gif) ………………9分
………………9分
∴P(x≥6)=.files\image160.gif) ………………12分
………………12分
答:线路信息畅通的概率为.files\image162.gif)
21.解:因为f′(x)=3x2+6ax+b,由题设得
.files\image164.gif)
解得:.files\image166.gif) ………………4分
………………4分
∴当.files\image168.gif) 时,f′(x)=3x2+6x+3=3(x+1)2≥0,于是f(x)不存在极值;
时,f′(x)=3x2+6x+3=3(x+1)2≥0,于是f(x)不存在极值;
当.files\image170.gif) 时,f′(x)=3x2+12x+9=3(x+1)(x+3),符合条件。 ………………6分
时,f′(x)=3x2+12x+9=3(x+1)(x+3),符合条件。 ………………6分
且f(1)=20, f(0)=4,于是由题设得:3x2+12x+9≤20m-8在区间[-4,3]上恒成立,又f′(x)=3x2+12x+9=3(x+2)2-3在区间 [-4,3]上的最大值为72.
∴.files\image172.gif) ,即实数m的取值范围是
,即实数m的取值范围是.files\image172.gif) .
.
22.(1)设M (x,y),则由.files\image074.gif) 且O是原点得
且O是原点得
A (2,0),B (2,1),C (0,1),从而.files\image175.gif) (x,y),
(x,y),.files\image177.gif)
.files\image179.gif)
由.files\image181.gif) 得(x,y)?(x-2,y)=k[(x,y-1)?(x-2,y-1)-|y-1|2]
得(x,y)?(x-2,y)=k[(x,y-1)?(x-2,y-1)-|y-1|2]
即(1-k)x2+2(k-1)x+y2=0为所求轨迹方程 ………………4分
①当k=1时,y=0动点M的轨迹是一条直线
②当k≠1时,(x-1)2+.files\image183.gif)
k=0时,动点M轨迹是一个圆
k>1时,动点M轨迹是一条双曲线;
0<k<1或k<0时轨迹是一个椭圆 . ………………6分
(2)当k=.files\image005.gif) 时,动点M的轨迹方程为(x-1)2+2y2=1即y2=
时,动点M的轨迹方程为(x-1)2+2y2=1即y2=.files\image005.gif) -
-.files\image005.gif) (x-1)2
(x-1)2
从而.files\image187.gif)
又由(x-1)2+2y2=1 ∴0≤x≤2
∴当x=.files\image189.gif) 时,
时,.files\image191.gif) 的最大值为
的最大值为.files\image193.gif) .
.
当x=0时,.files\image191.gif) 的最大值为16.
的最大值为16.
∴.files\image196.gif) 的最大值为4,最小值为
的最大值为4,最小值为.files\image198.gif) …………………10分
…………………10分
(3)由.files\image200.gif) 由
由.files\image202.gif) 得
得
①当0<k<1时,a2=1,b2=1-k,c2=k
∴e2=k ∴.files\image204.gif)
②当k<0时,e2=.files\image206.gif)
∴k∈.files\image208.gif) …………………14分
…………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com