
题目列表(包括答案和解析)
| BF | CD |

|
| 1 |
| 2 |
|
|
|
阅读材料:如图①,△ABC与△DEF都是等腰直角三角形,∠ACB=∠EDF=900,且点D 在AB边上,AB、EF的中点均为O,连结BF、CD、CO,显然点C、F、O在同一条直线上,可以证明△BOF≌△COD,则BF=CD。
解决问题:
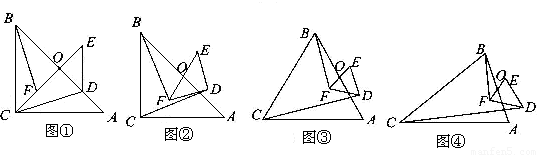
(1)将图①中的Rt△DEF绕点O旋转得到图②,猜想此时线段BF与CD的数量关系,并证明你的结论;
(2)如图③,若△ABC与△DEF都是等边三角形,AB、EF的中点均为O,上述(1)中结论仍然成立吗?如果成立,请说明理由;如果不成立,请求出BF与CD之间的数量关系;
(3)如图④,若△ABC与△DEF都是等腰三角形,AB、EF的中点均为O,且顶角∠ACB=∠EDF=α,请直接写出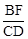 的值(用含α的式子表示出来)。
的值(用含α的式子表示出来)。
阅读材料

如图①,△ABC与△DEF都是等腰直角三角形,ACB=∠EDF=90°,且点D在AB边上,AB、EF的中点均为O,连结BF、CD、CO,显然点C、F、O在同一条直线上,可以证明△BOF≌△COD,则BF=CD.解决问题:
(1)将图①中的Rt△DEF绕点O旋转得到图②,猜想此时线段BF与CD的数量关系,并证明你的结论;
(2)如图③,若△ABC与△DEF都是等边三角形,AB、EF的中点均为O,上述(1)中的结论仍然成立吗?如果成立,请说明理由;如不成立,请求出BF与CD之间的数量关系;
(3)如图④,若△ABC与△DEF都是等腰三角形,AB、EF的中点均为0,且顶角∠ACB=∠EDF=α,请直接写出 的值(用含α的式子表示出来)
的值(用含α的式子表示出来)
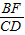 的值(用含α的式子表示出来)
的值(用含α的式子表示出来)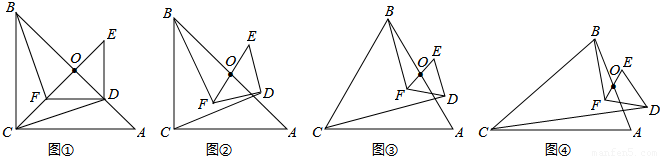
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com