
题目列表(包括答案和解析)
材料:在高一物理学习中,我们学习过力的分解,一个力可以分解为平面内任意两个方向上的力.如下图,
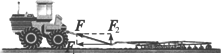
拖拉机拉着耙,对耙的拉力是斜向上方的,我们可以说,这个力产生两个效果:使耙克服泥土的阻力前进,同时把耙向上提,使它不会插得太深.这两个效果相当于两个力分别产生的:一个水平的力F1使耙前进,一个竖直向上的力F2把耙上提,即力F可以用两个力F1和F2来代替,即力F被分解成两个力F1和F2.
利用你所学知识,能不能将上面的物理知识抽象为数学知识?这一数学知识有何作用?
设函数
(1)当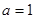 时,求曲线
时,求曲线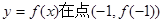 处的切线方程;
处的切线方程;
(2)当 时,求
时,求 的极大值和极小值;
的极大值和极小值;
(3)若函数 在区间
在区间 上是增函数,求实数
上是增函数,求实数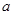 的取值范围.
的取值范围.
【解析】(1)中,先利用 ,表示出点
,表示出点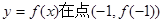 的斜率值
的斜率值 这样可以得到切线方程。(2)中,当
这样可以得到切线方程。(2)中,当 ,再令
,再令 ,利用导数的正负确定单调性,进而得到极值。(3)中,利用函数在给定区间递增,说明了
,利用导数的正负确定单调性,进而得到极值。(3)中,利用函数在给定区间递增,说明了 在区间
在区间 导数恒大于等于零,分离参数求解范围的思想。
导数恒大于等于零,分离参数求解范围的思想。
解:(1)当 ……2分
……2分
 ∴
∴
即 为所求切线方程。………………4分
为所求切线方程。………………4分
(2)当
令 ………………6分
………………6分
∴ 递减,在(3,+
递减,在(3,+ )递增
)递增
∴ 的极大值为
的极大值为 …………8分
…………8分
(3)
①若 上单调递增。∴满足要求。…10分
上单调递增。∴满足要求。…10分
②若
∵ 恒成立,
恒成立,
 恒成立,即a>0……………11分
恒成立,即a>0……………11分
 时,不合题意。综上所述,实数
时,不合题意。综上所述,实数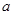 的取值范围是
的取值范围是
用数学归纳法证明:
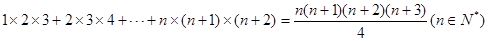 .
.
【解析】首先证明当n=1时等式成立,再假设n=k时等式成立,得到等式
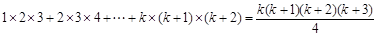 ,
,
下面证明当n=k+1时等式左边
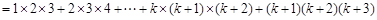 ,
,
根据前面的假设化简即可得到结果,最后得到结论.
| a2 |
| x |
| b2 |
| y |
| (a+b)2 |
| x+y |
| 2 |
| x |
| 9 |
| 1-2x |
| 1 |
| 2 |
 成立.
成立. 的最小值,并指出此时x的值.
的最小值,并指出此时x的值.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com