
题目列表(包括答案和解析)
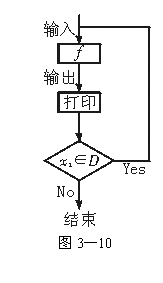
对任意函数f(x), x∈D,可按图示构造一个数列发生器,其工作原理如下:
①输入数据x0∈D,经数列发生器输出x1=f(x0);
②若x1![]() D,则数列发生器结束工作;若x1∈D,则将x1反馈回输入端,再输出x2=f(x1),并依此规律继续下去.
D,则数列发生器结束工作;若x1∈D,则将x1反馈回输入端,再输出x2=f(x1),并依此规律继续下去.
现定义![]()
(1)若输入x0=![]() ,则由数列发生器产生数列{xn},请写出{xn}的所有项;
,则由数列发生器产生数列{xn},请写出{xn}的所有项;
(2)若要数列发生器产生一个无穷的常数列,试求输入的初始数据x0的值;
(3)若输入x0时,产生的无穷数列{xn},满足对任意正整数n均有xn<xn+1;求x0的取值范围.
对任意函数 ,可按流程图构造一个数列发生器,其工作原理如下:①输入数据
,可按流程图构造一个数列发生器,其工作原理如下:①输入数据 ,数列发生器输出
,数列发生器输出 ;②若
;②若 ,则数列发生器结束工作;若
,则数列发生器结束工作;若 ,则将
,则将 反馈回输入端再输出
反馈回输入端再输出 ,并且依此规律继续下去.现定义
,并且依此规律继续下去.现定义 .
.
(1)若输入 ,则由数列发生器产生数列
,则由数列发生器产生数列 ,请写出数列
,请写出数列 的所有项;
的所有项;
(2)若要数列发生器产生一个无穷的常数数列,试求输入的初始数据 的值;
的值;
(3)若输入 时,产生的无穷数列
时,产生的无穷数列 满足:对任意正整数
满足:对任意正整数 ,均有
,均有 ,求
,求 的
的
取值范围.
 ,可按流程图构造一个数列发生器,其工作原理如下:①输入数据
,可按流程图构造一个数列发生器,其工作原理如下:①输入数据 ,数列发生器输出
,数列发生器输出 ;②若
;②若 ,则数列发生器结束工作;若
,则数列发生器结束工作;若 ,则将
,则将 反馈回输入端再输出
反馈回输入端再输出 ,并且依此规律继续下去.现定义
,并且依此规律继续下去.现定义 .
. ,则由数列发生器产生数列
,则由数列发生器产生数列 ,请写出数列
,请写出数列 的所有项;
的所有项; 的值;
的值; 时,产生的无穷数列
时,产生的无穷数列 满足:对任意正整数
满足:对任意正整数 ,均有
,均有 ,求
,求 的
的
 ①输入数据x0∈D,经数列发生器输出x1=f(x0);
①输入数据x0∈D,经数列发生器输出x1=f(x0);
②若x1![]() D,则数列发生器结束工作;若x1∈D,则将x1反馈回输入端,再输出x2=f(x1),并依此规律继续下去.
D,则数列发生器结束工作;若x1∈D,则将x1反馈回输入端,再输出x2=f(x1),并依此规律继续下去.
现定义f(x)=![]() .
.
(Ⅰ)若输入x0=![]() ,则由数列发生器产生数列{xn}.请写出数列{xn}的所有项;
,则由数列发生器产生数列{xn}.请写出数列{xn}的所有项;
(Ⅱ)若要数列发生器产生一个无穷的常数列,试求输入的初始数据x0的值;
(Ⅲ)(理)若输入x0时,产生的无穷数列{xn}满足:对任意正整数n,均有xn<xn+1,求x0的取值范围.
对任意函数f(x),x∈D,可按图示构造一个数列发生器,其工作原理如下:
(1)输入数据x0∈D,经数列发生器输出x1=f(x0).
(2)若x1![]() D,则数列发生器结束工作;若x1∈D,则将x1反馈输入端,再输出x2=f(x1),…
D,则数列发生器结束工作;若x1∈D,则将x1反馈输入端,再输出x2=f(x1),…
依此规律继续下去,现定义f(x)=![]() .
.
(1)若输入x0=![]() ,则由数列发生器产生数列{xn},请写出数列{xn}的所有项.
,则由数列发生器产生数列{xn},请写出数列{xn}的所有项.
(2)若要数列发生器产生一个无穷的常数列,试求输入的初始数据x0的值.
(3)若输入x0时,产生的无穷数列{xn}满足:对任一正整数n,均有xn<xn+1,求x0的取值范围.

1.B 2.C 3.B 4.C 5.B 6.B 7.C 8.B 9.C 10.B
11.C 12.D
【解析】
3.当文科数学.files/image290.gif) 时,函数
时,函数文科数学.files/image026.gif) 在
在文科数学.files/image028.gif) 上,
上,文科数学.files/image030.gif) 恒成立即
恒成立即文科数学.files/image295.gif) 在
在文科数学.files/image028.gif) 上恒成立,可得
上恒成立,可得文科数学.files/image298.gif)
当文科数学.files/image300.gif) 时,函数
时,函数文科数学.files/image026.gif) 在
在文科数学.files/image028.gif) 上,
上,文科数学.files/image030.gif) 恒成立
恒成立
即文科数学.files/image305.gif) 在
在文科数学.files/image028.gif) 上恒成立
上恒成立
可得文科数学.files/image308.gif) ,对于任意
,对于任意文科数学.files/image310.gif) 恒成立
恒成立
所以文科数学.files/image312.gif) ,综上得
,综上得文科数学.files/image314.gif) .
.
4.解法一:联立文科数学.files/image316.gif) ,得
,得文科数学.files/image318.gif) .
.
文科数学.files/image320.gif) 方程总有解,需
方程总有解,需文科数学.files/image322.gif) 恒成立
恒成立
即文科数学.files/image324.gif) 恒成立,得
恒成立,得文科数学.files/image326.gif) 恒成立
恒成立
文科数学.files/image328.gif) ;又
;又文科数学.files/image330.gif)
文科数学.files/image332.gif) 的取值范围为
的取值范围为文科数学.files/image334.gif) .
.
解法二:数形结合,因为直线文科数学.files/image040.gif) 恒过定点(0,1),要使直线与椭圆
恒过定点(0,1),要使直线与椭圆文科数学.files/image042.gif) 总有交点当日仅当点(0,1)在椭圆上或椭圆内,即
总有交点当日仅当点(0,1)在椭圆上或椭圆内,即文科数学.files/image338.gif)
文科数学.files/image340.gif) 又
又文科数学.files/image330.gif)
文科数学.files/image332.gif) 的取值范围为
的取值范围为文科数学.files/image334.gif) .
.
5.文科数学.files/image345.gif)
7.展开式前三项的系数满足文科数学.files/image347.gif) 可解得
可解得文科数学.files/image349.gif) ,或
,或文科数学.files/image351.gif) (舍去).从而可知有理项为
(舍去).从而可知有理项为文科数学.files/image353.gif) ,故C正确.
,故C正确.
8.文科数学.files/image355.gif) ,欲使
,欲使文科数学.files/image012.gif) 为奇函数,须使
为奇函数,须使文科数学.files/image358.gif) ,观察可知,
,观察可知,文科数学.files/image149.gif) 、
、文科数学.files/image153.gif) 不符合要求,若
不符合要求,若文科数学.files/image362.gif) ,则
,则文科数学.files/image364.gif)
文科数学.files/image366.gif) ,其在
,其在文科数学.files/image070.gif) 上是减函数,故B正确
上是减函数,故B正确
当文科数学.files/image369.gif) 时,
时,文科数学.files/image371.gif) ,其在
,其在文科数学.files/image070.gif) 上是增函数,不符合要求.
上是增函数,不符合要求.
9.文科数学.files/image082.gif) 等价于
等价于
文科数学.files/image375.gif)
画图可知文科数学.files/image377.gif) ,故
,故文科数学.files/image379.gif) .
.
10.如图乙所示.设文科数学.files/image381.gif) ,点
,点文科数学.files/image104.gif) 到直线
到直线文科数学.files/image091.gif) 的距离为
的距离为文科数学.files/image385.gif) ,则由抛物线定义得
,则由抛物线定义得文科数学.files/image387.gif) ,
,
文科数学.files/image389.jpg)
又由点文科数学.files/image104.gif) 在椭圆上,及椭圆第一定义得
在椭圆上,及椭圆第一定义得文科数学.files/image392.gif)
由椭圆第二定义得文科数学.files/image394.gif) ,解之得
,解之得文科数学.files/image396.gif) .
.
11.从52张牌中任意取13张牌的全部取法为文科数学.files/image398.gif) ;缺少某一种花色的取法为
;缺少某一种花色的取法为文科数学.files/image400.gif) ,缺少两种花色的取法为
,缺少两种花色的取法为文科数学.files/image402.gif) ,缺少三种花色的取法为
,缺少三种花色的取法为文科数学.files/image404.gif) ,根据容斥原理可知四种花色齐全的取法为
,根据容斥原理可知四种花色齐全的取法为文科数学.files/image406.gif) .
.
12.设文科数学.files/image126.gif) 中点为
中点为文科数学.files/image226.gif) ,连
,连文科数学.files/image410.gif) .由已知得
.由已知得文科数学.files/image412.gif) 平面
平面文科数学.files/image130.gif) ,作
,作文科数学.files/image415.gif) ,交
,交文科数学.files/image417.gif) 的延长线于点
的延长线于点文科数学.files/image419.gif) ,连
,连文科数学.files/image421.gif) .则
.则文科数学.files/image423.gif) 为所求,设
为所求,设文科数学.files/image425.gif) ,则
,则文科数学.files/image427.gif) ,在
,在文科数学.files/image429.gif)
中可求出文科数学.files/image431.gif) ,则
,则文科数学.files/image433.gif) .
.
二、填空题
13.文科数学.files/image435.gif) .
.
提示:可以用换元法,原不等式为文科数学.files/image437.gif) 也可以用数形结合法.
也可以用数形结合法.
令文科数学.files/image439.gif) ,在同一坐标系内分别画出这两个函数的图象,由图直观得解集.
,在同一坐标系内分别画出这两个函数的图象,由图直观得解集.
14.12文科数学.files/image441.gif) .提示:经判断,
.提示:经判断,文科数学.files/image266.gif) 为截面团的直径,再由巳知可求出球的半径为
为截面团的直径,再由巳知可求出球的半径为文科数学.files/image060.gif) .
.
15.文科数学.files/image445.gif) .提示:由于
.提示:由于文科数学.files/image447.gif) 得
得文科数学.files/image449.gif)
解得文科数学.files/image451.gif) ,又
,又文科数学.files/image453.gif)
文科数学.files/image455.gif)
所以,当文科数学.files/image457.gif) 时,
时,文科数学.files/image459.gif) 取得最小值.
取得最小值.
16.①②④
三、解答题
17.懈:文科数学.files/image461.gif)
文科数学.files/image463.gif) ,由正弦定理得,
,由正弦定理得,文科数学.files/image465.gif)
文科数学.files/image467.gif)
文科数学.files/image469.gif) 又
又文科数学.files/image471.gif) ,
,
文科数学.files/image473.gif) ,化简得
,化简得文科数学.files/image475.gif)
文科数学.files/image477.gif) 为等边三角形.
为等边三角形.
说明;本题是向量和三角相结合的题目,既考查了向量的基本知识,又考查了三角的有关知识,三角形的形状既可由角确定。也可由边确定,因此既可从角入手,把边化为角;也可从边入手,把角化为边来判断三角形的形状.
18.解:(1)在第一次更换灯泡工作中,不需要更换灯泡的概率为文科数学.files/image479.gif) 需要更换2只灯泡的概率为
需要更换2只灯泡的概率为文科数学.files/image481.gif) .
.
(2)对该盏灯来说,在第1、2次都更换了灯泡的概率为文科数学.files/image483.gif) ,在第一次未更换灯泡而在第二次需要更换灯泡的概率为
,在第一次未更换灯泡而在第二次需要更换灯泡的概率为文科数学.files/image485.gif) ,故所求的概率为
,故所求的概率为文科数学.files/image487.gif) .
.
(3)当文科数学.files/image207.gif) 时,
时,
由(2)知第二次灯泡更换工作中,某盏灯更换的概率文科数学.files/image490.gif)
故至少换4只灯泡的概率为文科数学.files/image492.gif)
文科数学.files/image494.gif)
文科数学.files/image496.gif)
文科数学.files/image498.gif)
19.解:文科数学.files/image500.gif) ]
]
因为函数文科数学.files/image012.gif) 在
在文科数学.files/image503.gif) 处的切线斜率为
处的切线斜率为文科数学.files/image087.gif)
所以文科数学.files/image506.gif)
即文科数学.files/image508.gif) ①
①
又文科数学.files/image510.gif)
得文科数学.files/image512.gif) ②
②
(1)函数文科数学.files/image012.gif) 在
在文科数学.files/image218.gif) 时有极值
时有极值
文科数学.files/image516.gif) ③
③
解式①②③得文科数学.files/image518.gif)
所以文科数学.files/image520.gif) .
.
(2)因为函数文科数学.files/image012.gif) 在区间
在区间文科数学.files/image221.gif) 上单调递增,所以导函数
上单调递增,所以导函数文科数学.files/image524.gif) 在区间
在区间文科数学.files/image221.gif) 的值恒大于或等于零.
的值恒大于或等于零.
则文科数学.files/image527.gif)
得文科数学.files/image529.gif) ,所以实数
,所以实数文科数学.files/image188.gif) 的取值范围为
的取值范围为文科数学.files/image532.gif) .
.
20.解:(1)连接文科数学.files/image534.gif) 因为
因为文科数学.files/image230.gif) 平面
平面文科数学.files/image232.gif) ,平面
,平面文科数学.files/image538.gif) 平面
平面文科数学.files/image540.gif)
所以文科数学.files/image542.gif) ;又
;又文科数学.files/image242.gif) 为
为文科数学.files/image239.gif) 的中点,故
的中点,故文科数学.files/image226.gif) 为
为文科数学.files/image228.gif) 的中点
的中点
文科数学.files/image548.gif)
文科数学.files/image550.gif) 底面
底面文科数学.files/image120.gif)
文科数学.files/image553.gif) 为
为文科数学.files/image236.gif) 与底面
与底面文科数学.files/image120.gif) 所成的角
所成的角
在文科数学.files/image557.gif) 中,
中,文科数学.files/image559.gif)
文科数学.files/image561.gif)
文科数学.files/image563.jpg) 所以
所以文科数学.files/image236.gif) 与底面
与底面文科数学.files/image120.gif) 所成的角为45°.
所成的角为45°.
(2)解法一;如图建立直角坐标系文科数学.files/image567.gif)
则文科数学.files/image569.gif) ,
, 文科数学.files/image571.gif)
文科数学.files/image573.gif) 设
设文科数学.files/image244.gif) 点的坐标为
点的坐标为文科数学.files/image576.gif)
故文科数学.files/image578.gif)
文科数学.files/image580.gif)
文科数学.files/image582.gif)
文科数学.files/image584.gif)
文科数学.files/image586.gif) 点
点文科数学.files/image244.gif) 的坐标为
的坐标为文科数学.files/image589.gif)
文科数学.files/image591.gif)
故文科数学.files/image593.gif) .
.
解法二:文科数学.files/image595.gif) 平面
平面文科数学.files/image597.gif)
文科数学.files/image599.gif) ,又
,又文科数学.files/image248.gif)
文科数学.files/image602.gif) 平面
平面文科数学.files/image604.gif)
在正方形文科数学.files/image597.gif) 中,
中,文科数学.files/image607.gif)
文科数学.files/image609.gif) .
.
21.解:(1)设点文科数学.files/image149.gif) 、
、文科数学.files/image151.gif) 的坐标分别为
的坐标分别为文科数学.files/image613.gif) 、
、文科数学.files/image615.gif) ,点
,点文科数学.files/image264.gif) 的坐标为
的坐标为文科数学.files/image618.gif)
当文科数学.files/image620.gif) 时,设直线
时,设直线文科数学.files/image091.gif) 的斜率为
的斜率为文科数学.files/image275.gif)
文科数学.files/image624.gif) 直线
直线文科数学.files/image091.gif) 过点
过点文科数学.files/image256.gif)
文科数学.files/image628.gif) 的方程为
的方程为文科数学.files/image630.gif)
又已知文科数学.files/image632.gif) ①
①
文科数学.files/image634.gif) ②
②
文科数学.files/image636.gif) ③
③
文科数学.files/image638.gif) ④
④
∴式①一式②得
文科数学.files/image640.gif) ⑤
⑤
③式+式④得
文科数学.files/image642.gif) ⑥
⑥
∴由式⑤、式⑥及文科数学.files/image644.gif)
得点文科数学.files/image264.gif) 的坐标满足方程
的坐标满足方程
文科数学.files/image647.gif) ⑦
⑦
当文科数学.files/image649.gif) 时,
时,文科数学.files/image275.gif) 不存在,此时
不存在,此时文科数学.files/image091.gif) 平行于
平行于文科数学.files/image653.gif) 轴,因此
轴,因此文科数学.files/image266.gif) 的中点
的中点文科数学.files/image264.gif) 一定落在
一定落在文科数学.files/image657.gif) 轴上,即
轴上,即文科数学.files/image264.gif) 的坐标为
的坐标为文科数学.files/image660.gif) ,显然点
,显然点文科数学.files/image264.gif) (
(文科数学.files/image032.gif) ,0)满足方程⑦
,0)满足方程⑦
综上,点文科数学.files/image264.gif) 的坐标满足方程
的坐标满足方程文科数学.files/image647.gif)
设方程⑦所表示的曲线为文科数学.files/image666.gif)
则由文科数学.files/image668.gif) ,
,
得文科数学.files/image670.gif)
因为文科数学.files/image672.gif) ,又已知
,又已知文科数学.files/image258.gif) ,
,
所以当文科数学.files/image675.gif) 时.
时.文科数学.files/image677.gif) ,曲线
,曲线文科数学.files/image666.gif) 与椭圆
与椭圆文科数学.files/image153.gif) 有且只有一个交点
有且只有一个交点文科数学.files/image256.gif) ,
,
当文科数学.files/image682.gif) 时,
时,文科数学.files/image684.gif) ,曲线
,曲线文科数学.files/image666.gif) 与椭圆
与椭圆文科数学.files/image153.gif) 没有交点,因为(0,0)在椭圆内,又在曲线
没有交点,因为(0,0)在椭圆内,又在曲线文科数学.files/image666.gif) 上,所以曲线
上,所以曲线文科数学.files/image666.gif) 在椭圆内,故点
在椭圆内,故点文科数学.files/image264.gif) 的轨迹方程为
的轨迹方程为文科数学.files/image690.gif)
文科数学.files/image692.gif)
(2)由文科数学.files/image694.gif) 解得曲线
解得曲线文科数学.files/image666.gif) 与
与文科数学.files/image653.gif) 轴交于点(0,0),(0,
轴交于点(0,0),(0,文科数学.files/image188.gif) )
)
由文科数学.files/image699.gif) 解得曲线
解得曲线文科数学.files/image666.gif) 与
与文科数学.files/image657.gif) 轴交于点(0,0).(
轴交于点(0,0).(文科数学.files/image032.gif) ,0)
,0)
当文科数学.files/image703.gif) ,即点
,即点文科数学.files/image256.gif) 为原点时,(
为原点时,(文科数学.files/image032.gif) ,0)、(0,
,0)、(0,文科数学.files/image188.gif) )与(0.0)重合,曲线
)与(0.0)重合,曲线文科数学.files/image666.gif) 与坐标轴只有一个交点(0,0).
与坐标轴只有一个交点(0,0).
当文科数学.files/image709.gif) ,且
,且文科数学.files/image711.gif) ,即点
,即点文科数学.files/image256.gif) 不在椭圆
不在椭圆文科数学.files/image153.gif) 外且在除去原点的
外且在除去原点的文科数学.files/image653.gif) 轴上时,曲线
轴上时,曲线文科数学.files/image666.gif) 与坐标轴有两个交点(0,
与坐标轴有两个交点(0,文科数学.files/image188.gif) )与(0,0),同理,当
)与(0,0),同理,当
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com