
题目列表(包括答案和解析)
三.解答题:本大题共6个小题,共70分,解答应写出文字说明、证明过程或演算步骤.
17. (本题满分10分)
已知函数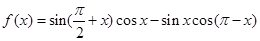 ,
,
(1)求函数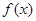 的最小正周期;
的最小正周期;
(2)在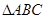 中,已知
中,已知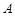 为锐角,
为锐角,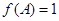 ,
,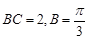 ,求
,求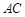 边的长.
边的长.
【必做题】(本题满分10分)
某单位举办2010年上海世博会知识宣传活动,进行现场抽奖.盒中装有9张大小相同的精美卡片,卡片上分别印有“世博会会徽”或“海宝”(世博会吉祥物)图案;抽奖规则是:参加者从盒中抽取卡片两张,若抽到两张都是‘‘海宝”,即可获奖,否则,均为不获奖.卡片用后后放同盒子,下一位参加者继续重复进行。
(I)有三人参加抽奖,要使至少一人获奖的概率不低于 ,则“海宝”卡至少多少张?
,则“海宝”卡至少多少张?
(2)若有四张“海宝”卡,现有甲乙丙丁四人依次抽奖.用 表示获奖的人数,求
表示获奖的人数,求 的分布列及E
的分布列及E 的值.
的值.
(本题满分10分)对某校高三年级学生参加社区服务次数进行统计,随机抽取 名学生作为样本,得到这
名学生作为样本,得到这 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
|
分组 |
频数 |
频率 |
|
|
10 |
0.25 |
|
|
24 |
|
|
|
|
|
|
|
2 |
0.05 |
|
合计 |
|
1 |
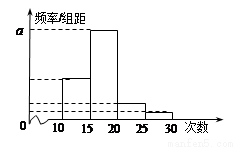
(Ⅰ)求出表中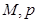 及图中
及图中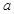 的值;
的值;
(Ⅱ)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间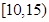 内的人数;
内的人数;
(Ⅲ)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间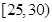 内的概率.
内的概率.
三、解答题(本大题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤)
17.(本题满分10分)
已知向量 ,
,  的夹角为
的夹角为 , 且
, 且 ,
,  , 若
, 若 ,
,  , 求(1)
, 求(1) ·
· ;
;
(2) .
.
三、解答题(本大题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤)
17.(本题满分10分)
已知向量 ,
,  的夹角为
的夹角为 , 且
, 且 ,
,  , 若
, 若 ,
,  , 求(1)
, 求(1) ·
· ;
;
(2) .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com