方法一:(Ⅰ)证明:在中..——青夏教育精英家教网—

方法一:(Ⅰ)证明:在中.. 【查看更多】

题目列表(包括答案和解析)

(1)证明：到直线的距离公式为．

(2)已知：在空间直角坐标系中，三元一次方程（其中为常数，且不全为零）表示平面，为该平面的一个法向量．请类比点到直线的距离公式，写出空间的点到平面的距离公式，并为加以证明．

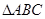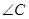命题“在中，若是直角，则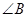一定是锐角．”的证明过程如下：

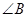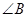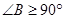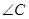假设不是锐角，则是直角或钝角，即，而是直角，

所以，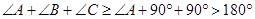

这与三角形的内角和等于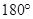矛盾，所以上述假设不成立，

即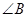一定是锐角．

本题采用的证明方法是（）

A. 综合法 B. 分析法 C. 反证法 D. 数学归纳法

（1）证明：P（x₀，y₀）到直线Ax+By+C=0的距离公式为d=

|Ax0+By0+C|

A2+B2

．
（2）已知：在空间直角坐标系中，三元一次方程Ax+By+Cz+D=0（其中A，B，C，D为常数，且A，B，C不全为零）表示平面，

=(A，B，C)为该平面的一个法向量．请类比点到直线的距离公式，写出空间的点P（x₀，y₀，z₀）到平面Ax+By+Cz+D=0的距离公式，并为加以证明．

（2009•崇明县二模）设椭圆C：

=1（a＞b＞0）的一个顶点坐标为A（0，-

），且其右焦点到直线y-x-2

=0的距离为3．
（1）求椭圆C的轨迹方程；
（2）若A、B是椭圆C上的不同两点，弦AB（不平行于y轴）的垂直平分线与x轴相交于点M，则称弦AB是点M的一条“相关弦”，如果点M的坐标为M（

，0），求证点M的所有“相关弦”的中点在同一条直线上；
（3）根据解决问题（2）的经验与体会，请运用类比、推广等思想方法，提出一个与“相关弦”有关的具有研究价值的结论，并加以解决．（本小题将根据所提出问题的层次性给予不同的分值）

4、命题“在△ABC中，若∠C是直角，则∠B一定是锐角．”的证明过程如下：
假设∠B不是锐角，则∠B是直角或钝角，即∠B≥90°，
所以∠A+∠B+∠C≥∠A+90°+90°＞180°，
这与三角形的内角和等于180°矛盾
所以上述假设不成立，所以∠B一定是锐角．
本题采用的证明方法是（　　）

A、数学归纳法

B、分析法

C、综合法

D、反证法

同步练习册答案