题目列表(包括答案和解析)
（1）若bk=am（m，k是大于2的正整数），求证：Sk-1=（m-1）a1;
（2）若b3=ai（i是某个正整数），求证：q是整数，且数列{bn}中的每一项都是数列｛an｝中的项。
（3）是否存在这样的正数q，使等比数列{bn}中有三项等差数列？若存在，写出一个q的值，并加以说明；若不存在，请说明理由。
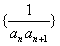的前n项和为Tn，求Tn。 在数列｛
｝中，
=1,an+1=2an+2n.
(Ⅰ)设bn=
.证明：数列｛bn｝是等差数列；
(Ⅱ)求数列｛an｝的前n项和Sn.
（Ⅰ）证明：12S3、S6、S12－S6成等比数列；
（Ⅱ）求和：Tn=a1+2a4+3a7+…+na3n－2.
已知数列｛an｝的前n项和为Sn，且满足an+ 2Sn·Sn-1=0(n≥2)，
．
(1)求证：
是等差数列；
(2)求an的表达式；
(3)若bn=2(1-n)an(n≥2)．求证：
+ …+ 
＜1
一：选择题：BCAAD CCCBA CC
二：填空题：
|
，
点A
不在两条高线
和
上，
，
，即
和
，
。
，
，
，
。
，因
，
在
上是增函数，
时，
，即
得
在（
，―1）递减，（―1，0）递增，
）递增。
处取得极小值，且
，使原方程有4个不同实根。
OF
AD，
，则EF
BC=B，
AEO为异面直线PD、AE所成的角
PD=1
，
，
， 
，
，令
，
在
递增
，可得实数
的取值范围为
时，
，
，
时，
，
，
，知
