
题目列表(包括答案和解析)
现有16张不同的卡片,其中红色、黄色、蓝色、绿色卡片各4张,从中任取3张,要求这些卡片不能是同一种颜色,且红色卡片至多1张,不同取法的种数为
(A)232 (B)252 (C)472 (D)484
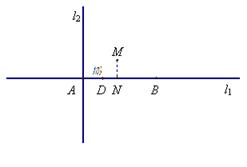
如图,直线l1与l2是同一平面内两条互相垂直的直线,交点是A,点B、D在直线l1上(B、D 位于点A右侧),且|AB|=4,|AD|=1,M是该平面上的一个动点,M在l1上的射影点是N,且|BN|=2|DM|.
(Ⅰ) 建立适当的坐标系,求动点M的轨迹C的方程.
(Ⅱ)过点D且不与l1、l2垂直的直线l交(Ⅰ)中的轨迹C于E、F两点;另外平面上的点G、H满足:①![]() ②
②![]() ③
③![]() 求点G的横坐标的取值范围.
求点G的横坐标的取值范围.
现有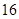 张不同的卡片,其中红色、黄色、蓝色、绿色卡片各
张不同的卡片,其中红色、黄色、蓝色、绿色卡片各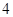 张.从中任取
张.从中任取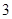 张,要求这
张,要求这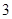 张卡片不能是同一种颜色,且红色卡片至多
张卡片不能是同一种颜色,且红色卡片至多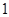 张.不同取法的种数为
张.不同取法的种数为
(A) (B)
(B)  (C)
(C)
 (D)
(D)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com