
题目列表(包括答案和解析)
图的曲线表示一个骑自行车离家的距离与时间的关系.骑车者9时离开家,15时回家,根据这个曲线图,请你回答下列头问题:
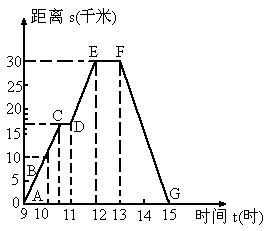
(1)最初到达离家最远的地方是什么时间?离家多远?
(2)何时开始第一次休息?休息多长时间?
(3)第一次休息时,离家多远?
(4)11∶00到12∶00他骑了多少千米?
(5)他在9∶00~10∶00和10∶00~10∶30的平均速度分别是多少?
(6)他在哪段时间里停止前进并休息用午餐?
图的曲线表示一个骑自行车离家的距离与时间的关系.骑车者
9时离开家,15时回家,根据这个曲线图,请你回答下列问题: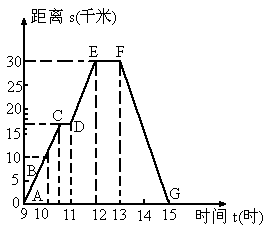
(1)最初到达离家最远的地方是什么时间?离家多远?
(2)
何时开始第一次休息?休息多长时间?(3)
第一次休息时,离家多远?(4)1
1∶00到12∶00他骑了多少千米?(5)
他在9∶00~10∶00和10∶00~10∶30的平均速度分别是多少?(6)
他在哪段时间里停止前进并休息用午餐?(本小题满分13分)
 某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30.第6小组的频数是7.
某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30.第6小组的频数是7.
(I) 求这次铅球测试成绩合格的人数;
(II) 用此次测试结果估计全市毕业生的情况.若从 今年的高中毕业生中随机抽取两名,记![]() 表示两人中成绩不合格的人数,求
表示两人中成绩不合格的人数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(III) 经过多次测试后,甲成绩在8~10米之间,乙成绩在9.5~10.5米之间,现甲、乙各投掷一次,求甲比乙投掷远的概率.
(本小题满分12分)
某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30.第6小组的频数是7.
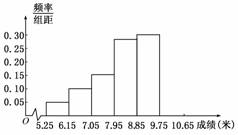 (1) 求这次铅球测试成绩合格的人数;
(1) 求这次铅球测试成绩合格的人数;
(2) 用此次测试结果估计全市毕业生的情况.若从今年的高中毕业生中随机抽取两名,记![]() 表示两人中成绩不合格的人数,求
表示两人中成绩不合格的人数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(3) 经过多次测试后,甲成绩在8~10米之间,乙成绩在9.5~10.5米之间,现甲、乙各投掷一次,求甲比乙投掷远的概率.
(本小题满分10分)
某食品公司为了解某种新品种食品的市场需求,进行了20天的测试,人为地调控每天产品的单价P(元/件):前10天每天单价呈直线下降趋势(第10天免费赠送品尝),后10天呈直线上升,其中4天的单价记录如下表:
|
时间(将第x天记为x) x |
1 |
10 |
11 |
18 |
|
单价(元/件)P |
9 |
0 |
1 |
8 |
而这20天相应的销售量Q(百件/天)与x对应的点(x,Q)在如图所示的半圆上.

(1)写出每天销售y(元)与时间x(天)的函数关系式y=f(x);
(2)在这20天中哪一天销售收入最高?为使每天销售收入最高,按此测试结果应将单价P设定为多少元为好?(结果精确到1元)
一、选择题(本大题共10小题,每小题4分,共40分)
1.B 2.C 3.D 4.C 5.A 6.C 7.B 8.A 9.C 10.A
二、填空题(本大题共4小题,每小题4分,共16分)
11.-4,13
12.75,83
13.203 722 104 088
三、解答题(本大题共3小题,共34分.)
15.(本题满分10分)
解:程序框图如下:

由其他算法得到的程序框图如果合理,请参照上面评分标准给分.
16.(本题满分12分)
解: 甲=
甲= (60+80+70+90+70)=74………………………………………………………………2分
(60+80+70+90+70)=74………………………………………………………………2分
 乙=
乙= (80+60+70+80+75)=73………………………………………………………………4分
(80+60+70+80+75)=73………………………………………………………………4分
s甲===2………………………………………………………………6分
s乙===2………………………………………………………………8分
∵ 甲>
甲> 乙,
乙, 甲>
甲> 乙………………………………………………………………10分
乙………………………………………………………………10分
∴甲的平均成绩较好,乙的各门功课发展较平衡………………………………………………………………12分
17.(本题满分12分)
解:(1)分别记白球为1,2,3号,黑球为4,5号.从口袋中每次任取一球,每次取出不放回,连续取两次,其一切可能的结果组成的基本事件(第一次摸到1号,第二次摸到2号球用(1,2)表示)空间为:Ω={(1,2),(2,1),(1,3),(3,1),(1,4),(4,1),(1,5),(5,1),(2,3),(3,2),(2,4),(4,2),(2,5),(5,2),(3,4),(4,3),(3,5),(5,3),(4,5),(5,4)},共有20个基本事件,且上述20个基本事件发生的可能性相同. ………………………………………………………………4分
记“取出的两只球都是白球”为事件A. ………………………………………………………………5分
A={(1,2),(2,1),(1,3),(3,1),(2,3),(3,2)},共有6个基本事件. ………………………………………7分
故P(A)==.
所以取出的两只球都是白球的概率为.………………………………………………………………8分
(2)设“取出的两只球中至少有一个白球”为事件B,则其对立事件为“取出的两只球均为黑球”. ………9分
={(4,5),(5,4)},共有2个基本事件. ………………………………………………………………10分
则P(B)=1-P()=1-=………………………………………………………………11分
所以取出的两只球中至少有一个白球的概率为………………………………………………………………12分
卷二
一、填空题(每小题4分,共16分)
1.1; 2.; 3.;4.6 500
二、解答题(本大题共2小题,共14分)
(本题8分)解:(1)从5张卡片中,任取两张卡片,其一切可能的结果组成的基本事件空间为Ω={(0,1),(0,2),(0,3),(0,4),(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)},共有10个基本事件,且这10个基本事件发生的可能性相同. ……1分
记“两张卡片上的数字之和等于
A={(0,4),(1,3)},共有2个基本事件. ………………………………………………………………2分
所以P(A)==………………………………………………………………3分
所以,从中任取两张卡片,两张卡片上的数字之和等于4的概率为…………………………………4分
(2)从5张卡片中,有放回地抽取两次卡片,其一切可能的结果组成的基本事件空间为Ω={(x,y)|x∈N,y∈N,0≤x≤4,0≤y≤4},共有25个基本事件. ……………5分
记“两次取出的卡片上的数字之和恰好等于
B={(0,4),(4,0),(1,3),(3,1),(2,2)},共有5个基本事件. ……………6分
则P(B)==……………7分
所以,两次取出的卡片上的数字之和恰好等于4的概率为……………8分
6.(本题6分)
解:(Ⅰ)语句“y=y+
y2 009是以2为公差的等差数列的第1 005项,所以y2 009=2+1 004×2=2 010……………2分
(2)语句“x=x+
xn+1=(k∈N*),其中x1=4;x2n+1=4x2n=4(x2n-1+3) ……………4分
即有x2n+1+4=4(x2n-1+4)令an=x2n-1+4,则数列{an}是以8为首项,4为公比的等比数列,所以an=8×4n-1=2×4n,所以x2n+1=2×4n+1-4
令x2n+1>22 008-4,即2×4n+1-4>22 008-4,所以22n+3>22 008,所以2n+3>2 008
即2n+1>2 006,易知输出框中的“n”即为上述的“2n+
因此输出的n值为2 007. ……………6分
其他正确解法按相应步骤给分.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com