
题目列表(包括答案和解析)
| OP |
| OA1 |
| OA2 |
| OP |
| OA1 |
| OA2 |
| OAn |
| OP |
| OA1 |
| OA2 |
| OAn |
| OP |
| OA1 |
| OA2 |
| OAn |
| a |
| 3 |
| b |
| 1 |
| 2 |
| ||
| 2 |
| m |
| a |
| b |
| n |
| a |
| b |
| m |
| n |
平面直角坐标系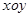 和极坐标系
和极坐标系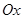 的原点与极点重合,
的原点与极点重合,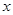 轴的正半轴与极轴重合,单位长度相同。已知曲线
轴的正半轴与极轴重合,单位长度相同。已知曲线 的极坐标方程为
的极坐标方程为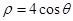 ,曲线
,曲线 的参数方程为
的参数方程为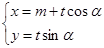
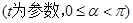 ,射线
,射线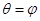 ,
,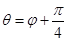 ,
,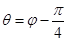 与曲线
与曲线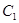 交于极点
交于极点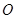 以外的三点A,B,C.
以外的三点A,B,C.
(1)求证: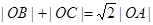 ;
;
(2)当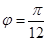 时,B,C两点在曲线
时,B,C两点在曲线 上,求
上,求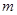 与
与 的值。
的值。
平面直角坐标系 和极坐标系
和极坐标系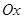 的原点与极点重合,
的原点与极点重合, 轴的正半轴与极轴重合,单位长度相同。已知曲线
轴的正半轴与极轴重合,单位长度相同。已知曲线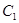 的极坐标方程为
的极坐标方程为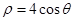 ,曲线
,曲线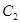 的参数方程为
的参数方程为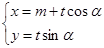
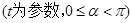 ,射线
,射线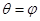 ,
,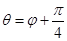 ,
,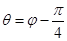 与曲线
与曲线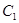 交于极点
交于极点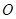 以外的三点A,B,C.
以外的三点A,B,C.
(1)求证: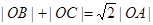 ;
;
(2)当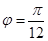 时,B,C两点在曲线
时,B,C两点在曲线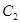 上,求
上,求 与
与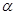 的值。
的值。
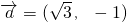 ,
,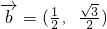 ,若存在不同时为o的实数k和x,使
,若存在不同时为o的实数k和x,使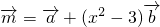 ,
,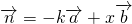 ,
, .
.一、选择题(每小题5分,共50分)
1.C 2.B 3.D 4.A 5.C 6.B 7.A 8.C 9.B 10.D
二、填空题(每小题4分,共24分)
11.84 12.(3,.files/image269.gif) ) 13.
) 13..files/image271.gif) 14.±2 15.1:2 16.4
14.±2 15.1:2 16.4
三、解答题(本大题共6小题,共76分)
17.(本题12分)
18.(本题12分)
解:(Ⅰ)记“甲投篮1次投进”为事件.files/image314.gif) ,“乙投篮1次投进”为事件
,“乙投篮1次投进”为事件.files/image316.gif) , “丙投篮1次投进”为事件
, “丙投篮1次投进”为事件.files/image318.gif) ,“3人都没有投进”为事件
,“3人都没有投进”为事件.files/image320.gif) ,
,
0
1
2
3
19.(本题12分)
解:以.files/image320.gif) 为坐标原点,射线
为坐标原点,射线.files/image364.gif) 分别为
分别为.files/image366.gif) 轴,
轴,.files/image368.gif) 轴,
轴,.files/image370.gif) 轴的正半轴建立如图所示的空间直角坐标系. ………………………(1分)
轴的正半轴建立如图所示的空间直角坐标系. ………………………(1分)
.files/image426.gif)
.files/image447.gif)
∴二面角B-PD-C大小为.files/image464.gif) 。 …………………………(12分)
。 …………………………(12分)
20.(本题12分)
∴只需 即 …………………………(5分)
21.(本题14分)
(Ⅱ)设直线.files/image </div>
</div>
<div class=)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com