
题目列表(包括答案和解析)
| 6 |
| 5π |
| π |
| 2 |
| 5π |
| 12 |
| π |
| 3 |
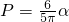 ,现有甲、乙、丙三门高射炮,每门高射炮击中目标与否相互独立,已知甲、乙、丙射击的角度分别为
,现有甲、乙、丙三门高射炮,每门高射炮击中目标与否相互独立,已知甲、乙、丙射击的角度分别为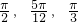 .
.| 3 | 4 |
| 3 |
| 4 |
 ,且只有3发子弹.该射手一旦射中目标,就停止射击,否则就一直独立地射击到子弹用完.设耗用子弹数为X,
,且只有3发子弹.该射手一旦射中目标,就停止射击,否则就一直独立地射击到子弹用完.设耗用子弹数为X,湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com