
题目列表(包括答案和解析)
下列命题中错误命题的个数为
①与两条异面直线都相交的两条直线是异面直线;②直线上有两点到平面的距离相等,则此直线与平面平行;③二面角的棱垂直于二面角的平面角所在的平面;④如果一个平面过另一个平面的斜线,那么这两个平面必不垂直.
[ ]
已知 是两个不同的平面,m,n是两条不同的直线,给出下列命题:( )
是两个不同的平面,m,n是两条不同的直线,给出下列命题:( )
①若 ;
;
②若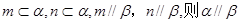 ;
;
③如果 是异面直线,那么
是异面直线,那么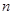 与
与 相交;
相交;
④若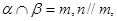 且
且 ,则
,则 且
且 其中正确的命题是( )
其中正确的命题是( )
A.①② B.①④ C.②③ D.③④
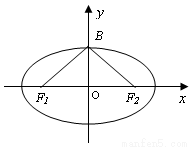
如图,已知椭圆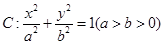 的焦点和上顶点分别为
的焦点和上顶点分别为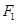 、
、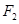 、
、 ,我们称
,我们称 为椭圆
为椭圆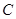 的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
(1)已知椭圆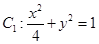 和
和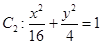 ,判断
,判断 与
与 是否相似,如果相似则求出
是否相似,如果相似则求出 与
与 的相似比,若不相似请说明理由;
的相似比,若不相似请说明理由;
(2)若与椭圆 相似且半短轴长为
相似且半短轴长为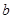 的椭圆为
的椭圆为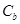 ,且直线
,且直线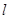 与椭圆为
与椭圆为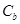 相交于两点
相交于两点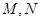 (异于端点),试问:当
(异于端点),试问:当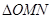 面积最大时,
面积最大时,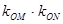 是否与
是否与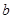 有关?并证明你的结论.
有关?并证明你的结论.
(3)根据与椭圆 相似且半短轴长为
相似且半短轴长为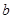 的椭圆
的椭圆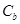 的方程,提出你认为有价值的相似椭圆之间的三种性质(不需证明);
的方程,提出你认为有价值的相似椭圆之间的三种性质(不需证明);
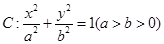 的焦点和上顶点分别为
的焦点和上顶点分别为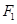 、
、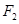 、
、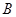 ,我们称
,我们称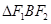 为椭圆
为椭圆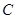 的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比. 和
和 ,判断
,判断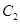 与
与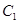 是否相似,如果相似则求出
是否相似,如果相似则求出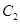 与
与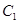 的相似比,若不相似请说明理由;
的相似比,若不相似请说明理由;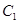 相似且半短轴长为
相似且半短轴长为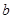 的椭圆为
的椭圆为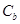 ,且直线
,且直线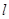 与椭圆为
与椭圆为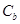 相交于两点
相交于两点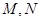 (异于端点),试问:当
(异于端点),试问:当 面积最大时,
面积最大时,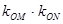 是否与
是否与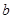 有关?并证明你的结论.
有关?并证明你的结论.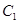 相似且半短轴长为
相似且半短轴长为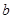 的椭圆
的椭圆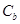 的方程,提出你认为有价值的相似椭圆之间的三种性质(不需证明);
的方程,提出你认为有价值的相似椭圆之间的三种性质(不需证明);
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com