
题目列表(包括答案和解析)
数列{an}满足an+1+(-1)n an =2n-1,则{an}的前60项和为
(A)3690 (B)3660 (C)1845 (D)1830
【解析】由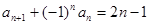 得,
得,
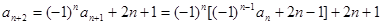
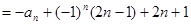 ,
,
即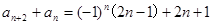 ,也有
,也有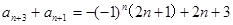 ,两式相加得
,两式相加得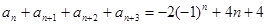 ,设
,设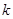 为整数,
为整数,
则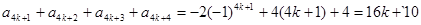 ,
,
于是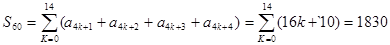
若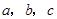 是不全相等的实数,求证:
是不全相等的实数,求证: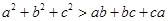 .
.
证明过程如下:
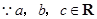 ,
,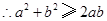 ,
,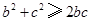 ,
,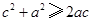 ,
,
又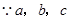 不全相等,
不全相等,
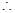 以上三式至少有一个“
以上三式至少有一个“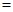 ”不成立,
”不成立,
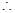 将以上三式相加得
将以上三式相加得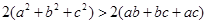 ,
,
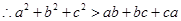 .
.
此证法是( )
A.分析法 B.综合法 C.分析法与综合法并用 D.反证法
22-12=2×1+1,
32-22=2×2+1,
42-32=2×3+1,
……
(n+1)2-n2=2n+1.
将以上各等式两边分别相加得(n+1)2-12=2(1+2+…+n)+n,即1+2+3+…+n=![]() .
.
(1)类比上述求法,请你求出12+22+32+…+n2的值.
(2)根据上述结论试求12+32+52+…+992的值.?
22-12=2×1+1,
32-22=2×2+1,
42-32=2×3+1,
……
(n+1)2-n2=2n+1.
将以上各等式两边分别相加得(n+1)2-12=2(1+2+…+n)+n,即1+2+3+…+n=![]() .
.
(1)类比上述求法,请你求出12+22+32+…+n2的值.
(2)根据上述结论试求12+32+52+…+992的值.?
若a,b,c是不全相等的实数,求证:a2+b2+c2>ab+bc+ca.
证明过程如下:
∵a、b、c∈R,∴a2+b2≥2ab,
b2+c2≥2bc,c2+a2≥2ac,
又∵a,b,c不全相等,
∴以上三式至少有一个“=”不成立,
∴将以上三式相加得2(a2+b2+c2)>2(ab+bc+ac),
∴a2+b2+c2>ab+bc![]() +ca.
+ca.
此证法是( )
(A)分析法 (B)综合法
(C)分析法与综合法并用 (D)反证法
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com