
题目列表(包括答案和解析)
| ||
| 2 |
| 2 |
| 1 |
| 2 |
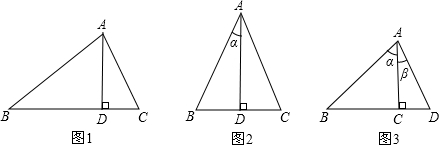
 ,90°是45°的两倍,但三角函数值却是
,90°是45°的两倍,但三角函数值却是 倍;
倍; ,
,
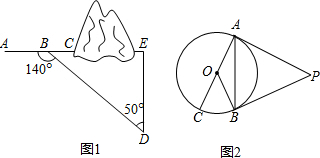
 ,cosA=
,cosA=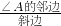 ,tanA=
,tanA= ,cotA=
,cotA=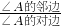
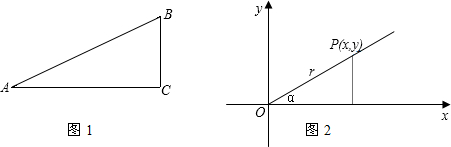
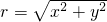 (r总是正的),然后把角α的三角函数规定为:
(r总是正的),然后把角α的三角函数规定为: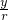 ,cosα=
,cosα=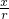 ,tanα=
,tanα= ,cotα=
,cotα=
 ),且cosα=
),且cosα=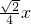 ,则tanα______;
,则tanα______;湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com