把乘法公式从右到左地使用，就可以把某些形式的多项式进行因式分解，这种方法叫做公式法，即
a²-b²=，a²±2ab+b²=．

由分解因式与整式乘法的关系可以看出，如果把乘法公式反过来，那么就可以用来把某些多项式分解因式，这种分解因式的方法叫做．

24、小刚同学动手剪了如图①所示的正方形与长方形纸片若干张．
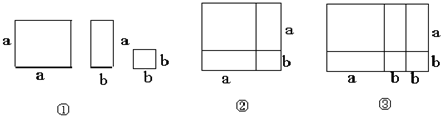
观察与操作：
（1）他拼成如图②所示的正方形，根据四个小纸片的面积之和等于大正方形的面积，得到：a²+2ab+b²=（a+b）²，验证了完全平方公式；即：多项式  a²+2ab+b² 分解因式后，其结果表示正方形的长（a+b）与宽（a+b）两个整式的积．
（2）当他拼成如图③所示的矩形，由面积相等又得到：a²+3ab+2b²=（a+2b）（a+b），即：多项式 a²+3ab+2b² 分解因式后，其结果表示矩形的长（a+2b）与宽（a+b）两个整式的积．
问题解决：
（1）请你依照小刚的方法，利用拼图分解因式：a²+4ab+3b²．（画图说明，并写出其结果）
（2）试猜想面积是2a²+5ab+3b²的矩形，其长与宽分别是多少？（画图说明，并写出其结果）