
题目列表(包括答案和解析)
| 1 | 2 |

抛物线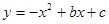 的部分图像如图所示,
的部分图像如图所示,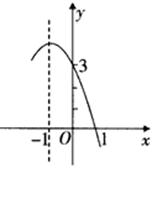
【小题1】(1)求出二次函数的解析式;
【小题2】(2)若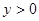 ,写出
,写出 的取值范围;
的取值范围;
【小题3】(3)将二次函数的图象在 轴上方的部分沿
轴上方的部分沿 轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线
轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线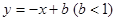 与此图象有两个公共点时,求
与此图象有两个公共点时,求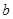 的取值范围.
的取值范围.
抛物线![]() 的部分图像如图所示,
的部分图像如图所示,
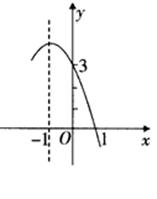
1.(1)求出二次函数的解析式;
2.(2)若![]() ,写出
,写出![]() 的取值范围;
的取值范围;
3.(3)将二次函数的图象在![]() 轴上方的部分沿
轴上方的部分沿![]() 轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线
轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线![]() 与此图象有两个公共点时,求
与此图象有两个公共点时,求![]() 的取值范围.
的取值范围.
抛物线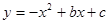 的部分图像如图所示,
的部分图像如图所示,
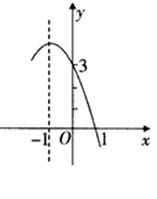
1.(1)求出二次函数的解析式;
2.(2)若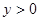 ,写出
,写出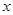 的取值范围;
的取值范围;
3.(3)将二次函数的图象在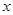 轴上方的部分沿
轴上方的部分沿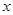 轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线
轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线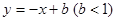 与此图象有两个公共点时,求
与此图象有两个公共点时,求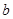 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com