
题目列表(包括答案和解析)
设函数![]() 给出下列四个命题:①
给出下列四个命题:①![]() 时,
时,![]() 是奇函数②
是奇函数②![]() 时,方程
时,方程![]() 只有一个实根③
只有一个实根③![]() 的图象关于
的图象关于![]() 对称 ④方程
对称 ④方程![]() 至多两个实根.其中正确的命题是
至多两个实根.其中正确的命题是
A.①、④ B.①、③ C.①、②、③ D.①、②、④
设函数 ,给出下列四个命题:
,给出下列四个命题:
① 时,
时, 是奇函数 ②
是奇函数 ② 时,方程
时,方程 只有一个实根
只有一个实根
③ 的图象关于
的图象关于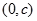 对称 ④方程
对称 ④方程 至多两个实数根
至多两个实数根
其中正确的命题的个数是( )
A.1 B. 2 C.3 D.4
设函数 ,给出下列四个命题:
,给出下列四个命题:
① 时,
时, 是奇函数 ②
是奇函数 ② 时,方程
时,方程 只有一个实根
只有一个实根
③ 的图象关于点
的图象关于点 对称 ④方程
对称 ④方程 至多两个实根
至多两个实根
其中正确的命题是( )
A.①④ B.①③ C.①②③ D.①②④
设函数 ,给出下列四个命题:
,给出下列四个命题:
① 时,
时, 是奇函数 ②
是奇函数 ②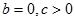 时,方程
时,方程 只有一个实根
只有一个实根
③ 的图象关于
的图象关于 对称 ④方程
对称 ④方程 至多两个实数根
至多两个实数根
其中正确的命题的个数是( )
| A.1 | B.2 | C.3 | D.4 |
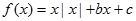 ,给出下列四个命题:
,给出下列四个命题: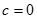 时,
时,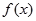 是奇函数 ②
是奇函数 ②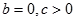 时,方程
时,方程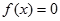 只有一个实根
只有一个实根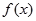 的图象关于
的图象关于 对称 ④方程
对称 ④方程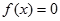 至多两个实数根
至多两个实数根| A.1 | B.2 | C.3 | D.4 |
一、选择题(每小题5分,共40分)
1-8.BACDD CCD
二、填空题(每小题5分,共30分)
9. 必要非充分
10. 4
11. 3
12.(e,e) 
13. x + 6 说明:f(x) = ax + 6 (a = 1,2,3,4,5)均满足条件.
14. 10 .
三、解答题(共80分)
15.(12分)
 .
.
16.(13分)
(1)当6≤t<9时. (2分)
(2分)
 (3分)
(3分)

 (5分)
(5分)
 (分钟)(6分)
(分钟)(6分)
(2)
∴ (分钟)(8分)
(分钟)(8分)
(3)

∴ (分钟)
(分钟)
综上所述,上午8时,通过该路段用时最多,为18.75分钟。(13分)
17.(13分)

 ,∴
,∴ (4分)
(4分)
 ∴
∴ (6分)
(6分)
“有且只有一个实数满足 ”,即抛物线
”,即抛物线 与x轴有且只有一个交点,
与x轴有且只有一个交点,
∴ ,∴
,∴ (10分)
(10分)
∴

∴ (13分)
(13分)
18.(14分)

19.(14分)
(1) ,∴
,∴ .
.
要使函数f(x)在定义域 内为单调函数,则在
内为单调函数,则在 内
内 恒大于0或恒小于0,
恒大于0或恒小于0,
当 在
在 内恒成立;
内恒成立;
当 要使
要使 恒成立,则
恒成立,则 ,解得
,解得 ,
,
当 要使
要使 恒成立,则
恒成立,则 ,解得
,解得 ,
,
所以 的取值范围为
的取值范围为 或
或 或
或 .
.
根据题意得: ,∴
,∴
于是 ,
,
用数学归纳法证明如下:
当
 ,不等式成立;
,不等式成立;
假设当 时,不等式
时,不等式 成立,即
成立,即 也成立,
也成立,
当 时,
时, ,
,
所以当 ,不等式也成立,
,不等式也成立,
综上得对所有 时5,都有
时5,都有 .
.
(3) 由(2)得 ,
,
于是
 ,
,
所以 ,
,
累乘得: ,
,
所以 .
.
20.(14分)
(1)∵定义域{x| x ≠ kπ,k∈Z }关于原点对称,
又f(- x) = f [(a - x) - a]= = = = = = - f (x),
对于定义域内的每个x值都成立
∴ f(x)为奇函数(4分)
(2)易证:f(x + 4a) = f(x),周期为
(3)f(2a)= f(a + a)= f [a -(- a)]= = = 0,
f(3a)=
f(
先证明f(x)在[
设
∴ f(x - 2a)= = - > 0,
∴ f(x)< 0(10分)
设2a < x1
< x2 <
则0 < x2 - x1 < a,∴ f(x1)< 0 f(x2)< 0 f(x2 - x1)> 0,
∴ f(x1)- f(x2)= > 0,
∴ f(x1)> f(x2),
∴ f(x)在[
∴ f(x)在[
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com