练习册

  • 练习册
  • 试题
    A． B．P＝T＝S 【查看更多】

     

    题目列表(包括答案和解析)

    椭圆C：(a＞b＞0)的一个焦点F1(－2，0)，右准线方程x＝8．

    (1)求椭圆C的方程；

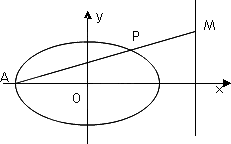
    (2)若M为右准线上一点，A为椭圆C的左顶点，连结AM交椭圆于点P，求的取值范围；

    (3)设圆Q：(x－t)2＋y2＝1(t＞4)与椭圆C有且只有一个公共点，过椭圆C上一点B作圆Q的切线BS、BT，切点为S，T，求·的最大值．

    查看答案和解析>>

    设椭圆T：(a＞b＞0)，直线l过椭圆左焦点F1且不与x轴重合，l与椭圆交于P、Q，左准线与x轴交于K，|KF1|＝2．当l与x轴垂直时，|PQ|＝．

    (1)求椭圆T的方程；

    (2)直线l绕着F1旋转，与圆O：x2＋y2＝5交于A，B两点，若|AB|∈[4，]，求△F2PQ的面积S的取值范围(F2为椭圆的右焦点)．

    查看答案和解析>>

    已知椭圆＝1(a＞b＞0)的左、右焦点分别为F1、F2，若以F2为圆心，b－c为半径作圆F2，过椭圆上一点P作此圆的切线，切点为T，且|PT|的最小值不小于(a－c)．

    (1)证明：椭圆上的点到F2的最短距离为a－c；

    (2)求椭圆的离心率e的取值范围；

    (3)设椭圆的短半轴长为1，圆F2与x轴的右交点为Q，过点Q作斜率为k(k＞0)的直线l与椭圆相交于A、B两点，若OA⊥OB，求直线l被圆F2截得的弦长S的最大值．

    查看答案和解析>>

    已知椭圆＋＝1(a＞b＞0)的左、右焦点分别是F1(－c，0)，F2(c，0)，Q是椭圆外的动点，满足||＝2a．点P是线段F1Q与该椭圆的交点，点T在线段F2Q上，并且满足·＝0，||≠0．

    (1)设x为点P的横坐标，证明||＝a＋x；

    (2)求点T的轨迹C的方程；

    (3)试问：在点T的轨迹C上，是否存在点M，使△F1MF2的面积S＝b2？若存在，求∠F1MF2的正切值；若不存在，请说明理由．

    查看答案和解析>>

    已知椭圆＋＝1(a＞b＞0)的左、右焦点分别是F1(－c，0)，F2(c，0)，Q是椭圆外的动点，满足||＝2a．点P是线段F1Q与该椭圆的交点，点T在线段F2Q上，并且满足·＝0，||≠0．

    (1)设x为点P的横坐标，证明||＝a＋x；

    (2)求点T的轨迹C的方程；

    (3)试问：在点T的轨迹C上，是否存在点M，使△F1MF2的面积S＝b2？若存在，求∠F1MF2的正切值；若不存在，请说明理由．

    查看答案和解析>>

    1．（理）A　（文）B　2．（理）B　（文）B　3．B　4．A　5．D　

    6．（理）B　（文）D　7．B　8．（理）C　（文）D　9．D　10．D　11．C

    12．（理）A　（文）A　13．1或0　14．　15．10080°　16．

    　　17．解析：（1）的分布如下

    0

    1

    2

    P

    　　（2）由（1）知．

    　　∴　．

    　　18．解析：（1）以点为坐标原点，所在直线为x轴，所在直线为z轴，建立空间直角坐标系，设，（a，（0，＋∞）．

    　　∵　三棱柱为正三棱柱，则，B，，C的坐标分别为：（b，0，0），，，，，，，（0，0，a）．　∴　　，，，，，．

    　　（2）在（1）条件下，不妨设b＝2，则，

    　　又A，M，N坐标分别为（b，0，a），（，，0），（，，a）．

    　　∴　，．　　∴　

    　　同理　．

    　　∴　△与△均为以为底边的等腰三角形，取中点为P，则，为二面角的平面角，而点P坐标为（1，0，），

    　　∴　，，．　同理　，，．

    　　∴　．

    　∴　∠NPM＝90°二面角的大小等于90°．

    　　19．解析：设派x名消防员前去救火，用t分钟将火扑灭，总损失为y，则

    　　y＝灭火劳务津贴＋车辆、器械装备费＋森林损失费

    　　 ＝125tx＋100x＋60（500＋100t）

    　　 ＝

    　　 ＝

    　　 ＝

    　　

    　　当且仅当，即x＝27时，y有最小值36450．

    　　故应该派27名消防员前去救火，才能使总损失最少，最少损失为36450元．

    　　20．解析：（1）当A、B、C三点不共线时，由三角形中线性质知

    ；

    　　当A，B，C三点共线时，由在线段BC外侧，由或x＝5，因此，当x＝1或x＝5时，有，

    　　同时也满足：．当A、B、C不共线时，

    定义域为[1，5]．

    　　（2）（理）∵　．　∴　d＝y＋x-1＝．

    　　令　t＝x-3，由，，

    　　两边对t求导得：关于t在[-2，2]上单调增．

    　　∴　当t＝2时，＝3，此时x＝1．　当t＝2时，＝7．此时x＝5．故d的取值范围为[3，7]．

    　　（文）由且，，

    　　∴　当x＝3时，．当x＝1或5时，．

    　　∴　y的取值范围为[，3]．

    　　21．解析：（1）令，令y＝-x，则

    在（-1，1）上是奇函数．

    　　（2）设，则，而，．即　当时，

    ．

    　　∴　f（x）在（0，1）上单调递减．

    　　（3）（理）由于，

    　　，，

    　　∴　．

    　　22．解析：（理）由平面，连AH并延长并BC于M．

    　　则　由H为△ABC的垂心．　∴　AM⊥BC．

    　　于是　BC⊥平面OAHOH⊥BC．

    　　同理可证：平面ABC．

    　　又　，，是空间中三个不共面的向量，由向量基本定理知，存在三个实数，，使得＝a＋b＋c．

    　　由　且＝＝0b＝c，　同理．

    　　∴　．　　　　　　　　　　　　①

    　　又　AH⊥OH，

    　　∴　＝0

    　　　　　　　　　　　　　　　　　　　　 ②

    　　联立①及②，得　　③

    　　又由①，得　，，，代入③得：

    　　，，，

    　　其中，于是．

    　　（文）（1）联立方程ax＋1＝y与，消去y得：　 （*）

    　　又直线与双曲线相交于A，B两点，　∴．

    　　又依题　OA⊥OB，令A，B两点坐标分别为（，），（，），则　．

    　　且　

    ，而由方程（*）知：，代入上式得．满足条件．

    　　（2）假设这样的点A，B存在，则l：y＝ax＋1斜率a＝-2．又AB中点，在上，则，

    　　又　，

    　　代入上式知　这与矛盾．

    　　故这样的实数a不存在．

     


    同步练习册答案