
题目列表(包括答案和解析)
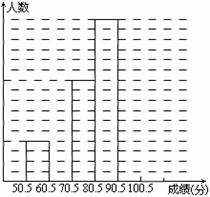
(本题满分14分)为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频数条形图,解答下列问题:
(Ⅰ)填充频率分布表的空格(将答案直接填在表格内);
(Ⅱ)补全频数条形图;
(Ⅲ)学校决定成绩在75.5~85.5分的学生为二等奖,问该校获得二等奖的学生约为多少人?
|
分组 |
频数 |
频率 |
|
50.5~60.5 |
4 |
0.08 |
|
60.5~70.5 |
|
0.16 |
|
70.5~80.5 |
10 |
|
|
80.5~90.5 |
16 |
0.32 |
|
90.5~100.5 |
|
|
|
合计 |
50 |
|

(本题满分14分)为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频数条形图,解答下列问题:
(Ⅰ)填充频率分布表的空格(将答案直接填在表格内);
(Ⅱ)补全频数条形图;
(Ⅲ)学校决定成绩在75.5~85.5分的学生为二等奖,问该校获得二等奖的学生约为多少人?
| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | | 0.16 |
| 70.5~80.5 | 10 | |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | | |
| 合计 | 50 | |
(本题14分)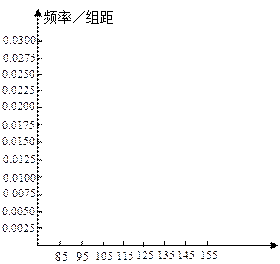 高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
| 分组 | 频数 | 频率 |
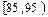 | ① | 0. 025 |
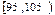 | | 0.050 |
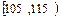 | | 0.200 |
 | 12 | 0.300 |
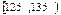 | | 0.275 |
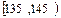 | 4 | ② |
| [145,155] | | 0.050 |
| 合计 | | ③ |
|
(本题14分)
 高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
| 分组 | 频数 | 频率 |
|
| ① | 0. 025 |
|
| 0.050 | |
|
| 0.200 | |
|
| 12 | 0.300 |
|
| 0.275 | |
|
| 4 | ② |
| [145,155] | 0.050 | |
| 合计 | ③ |
|
(1)根据上面图表,①②③处的数值分别为 ▲ ▲ ▲ ;
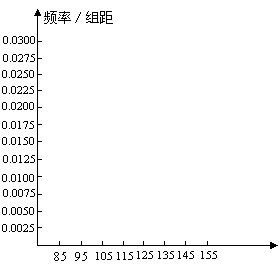
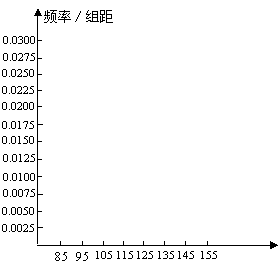
(2)在所给的坐标系中画出[85,155]的频率分布直方图;
(3)根据题中信息估计总体落在[125,155]中的概率.
(本题14分)
 高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
| 分组 | 频数 | 频率 |
|
| ① | 0. 025 |
|
| 0.050 | |
|
| 0.200 | |
|
| 12 | 0.300 |
|
| 0.275 | |
|
| 4 | ② |
| [145,155] | 0.050 | |
| 合计 | ③ |
|
(1)根据上面图表,①②③处的数值分别为 ▲ 、 ▲ 、 ▲ ;
(2)在所给的坐标系中画出[85,155]的频率分布直方图;
(3)根据题中信息估计总体落在[125,155]中的概率.
一、选择题:本大题共10小题,每小题5分,共50分.
题号
1
2
3
4
5
6
7
8
9
10
解答
D
D
A
B
D
C
C
B
D
D
二、填空题:本大题共7小题,每小题4分,共28分
11. 负
12. 
13. 7 14. 
15. 4010
16. 
17.若他不放弃这5道题,则这5道题得分的期望为:
三、解答题:本大题共5小题,共72分.解答应写出文字说明,证明过程或演算步骤.
18.解:(Ⅰ)①,②,③,④处的数值分别为:3,0.025,0.100,1.…………4分
(Ⅱ)
…………………………………………………………………………8分
(Ⅲ)(?)120分及以上的学生数为:(0.275+0.100+0.050)×5000=2125;
(?)平均分为:

(?)成绩落在[126,150]中的概率为:
…………………………………………………………………………14分
19.解:(Ⅰ) 由三视图可知,四棱锥 的底面是边长为1的正方形,
的底面是边长为1的正方形,
侧棱 底面
底面 ,且
,且 .
.
∴ ,
,
即四棱锥 的体积为
的体积为 .
………………………………4分
.
………………………………4分
(Ⅱ) 不论点 在何位置,都有
在何位置,都有 .
.
证明如下:连结 ,∵
,∵ 是正方形,∴
是正方形,∴ .
.
∵ 底面
底面 ,且
,且 平面
平面 ,∴
,∴ .
.
又∵ ,∴
,∴ 平面
平面 .
.
∵不论点 在何位置,都有
在何位置,都有
 平面
平面 .
.
∴不论点 在何位置,都有
在何位置,都有 . ………………………………8分
. ………………………………8分
(Ⅲ) 解法1:在平面 内过点
内过点 作
作 于
于 ,连结
,连结 .
.
 ∵
∵ ,
, ,
, ,
,
∴Rt△ ≌Rt△
≌Rt△ ,
,
从而△ ≌△
≌△ ,∴
,∴ .
.
∴ 为二面角
为二面角 的平面角.
的平面角.
在Rt△ 中,
中, ,
,
又 ,在△
,在△ 中,由余弦定理得
中,由余弦定理得
 ,
,
∴ ,即二面角
,即二面角 的大小为
的大小为 . …………………14分
. …………………14分
解法2:如图,以点 为原点,
为原点, 所在的直线分别为
所在的直线分别为 轴建立空间直角
轴建立空间直角
坐标系. 则 ,从而
,从而
 ,
, ,
, ,
, .
.
 设平面
设平面 和平面
和平面 的法向量分别为
的法向量分别为
 ,
, ,
,
由 ,取
,取 .
.
由 ,取
,取 .
.
设二面角 的平面角为
的平面角为 ,
,
则 ,
,
∴ ,即二面角
,即二面角 的大小为
的大小为 . …………………14分
. …………………14分
20.解:(Ⅰ)令 ①
①
令 ②
②
由①、②知, ,又
,又 是
是 上的单调函数,
上的单调函数,

 . ………………………………………………………………………4分
. ………………………………………………………………………4分
(Ⅱ) ,
,

 .
.



 ,
,
 …………………………………………………………………10分
…………………………………………………………………10分
(Ⅲ)令 ,则
,则

 ……………………12分
……………………12分
 对
对 都成立
都成立


…………………………………………………………………………………15分
21.解:(Ⅰ)设B( ,
, ),C(
),C( ,
,
 ),BC中点为(
),BC中点为( ),F(2,0).
),F(2,0).
则有 .
.
两式作差有

 .
.
设直线BC的斜率为 ,则有
,则有
 . (1)
. (1)
因F2(2,0)为三角形重心,所以由 ,得
,得
由 得
得 ,
,
代入(1)得 .
.
直线BC的方程为 .
…………………………………………7分
.
…………………………………………7分
(Ⅱ)由AB⊥AC,得 (2)
(2)
设直线BC方程为 ,得
,得

 ,
,


代入(2)式得, ,
,
解得 或
或
故直线 过定点(0,
过定点(0, . …………………………………………14分
. …………………………………………14分
22.解:(Ⅰ)

 .
.

当 时,
时,
 .从而有
.从而有 .…………………5分
.…………………5分
(Ⅱ)设P ,切线
,切线 的倾斜角分别为
的倾斜角分别为 ,斜率分别为
,斜率分别为 .则
.则
 .
.
由切线 与
与 轴围成一个等腰三角形,且
轴围成一个等腰三角形,且 均为正数知,该三角形为钝角三角形,
均为正数知,该三角形为钝角三角形,

 或
或 

 .又
.又

 .从而,
.从而, .
.

…………………………………………………………………………………10分
(Ⅲ)令

 ;
;
 .
.
 .
.
又 .
.


 .
.
当 时,即
时,即 时,曲线
时,曲线 与曲线
与曲线 无公共点,故方程
无公共点,故方程 无实数根;
无实数根;
当 时,即
时,即 时,曲线
时,曲线 与曲线
与曲线 有且仅有1个公共点,故方程
有且仅有1个公共点,故方程 有且仅有1个实数根;
有且仅有1个实数根;
当 时,即
时,即 时,曲线
时,曲线 与曲线
与曲线 有2个交点,故方程
有2个交点,故方程 有2个实数根.
…………………………………………………………………15分
有2个实数根.
…………………………………………………………………15分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com