练习册

  • 练习册
  • 试题
    宁波市八校联考高三数学试题答题卷题号12345678910解答 【查看更多】

     

    题目列表(包括答案和解析)

    （2012•惠州一模）甲乙两个学校高三年级分别有1200人，1000人，为了了解两个学校全体高三年级学生在该地区六校联考的数学成绩情况，采用分层抽样方法从两个学校一共抽取了110名学生的数学成绩，并作出了频数分布统计表如下：
    甲校：
    分组 [70，80） [80，90） [90，100） [100，110）
    频数 3 4 8 15
    分组 [110，120） [120，130） [130，140） [140，150]
    频数 15 x 3 2
    乙校：
    分组 [70，80） [80，90） [90，100） [100，110）
    频数 1 2 8 9
    分组 [110，120） [120，130） [130，140） [140，150]
    频数 10 10 y 3
    （Ⅰ）计算x，y的值．
    甲校 乙校 总计
    优秀
    非优秀
    总计
    （Ⅱ）若规定考试成绩在[120，150]内为优秀，请分别估计两个学校数学成绩的优秀率．
    （Ⅲ）由以上统计数据填写右面2×2列联表，并判断是否有90%的把握认为两个学校的数学成绩有差异．
    参考数据与公式：
    由列联表中数据计算K2=
    n(ad-bc)2
    (a+b)(c+d)(a+c)(b+d)

    临界值表
    P（K≥k0） 0.10 0.05 0.010
    k0 2.706 3.841 6.635

    查看答案和解析>>

    （本小题满分12分）甲乙两个学校高三年级分别有1200人，1000人，为了了解两个学校全体高三年级学生在该地区六校联考的数学成绩情况，采用分层抽样方法从两个学校一共抽取了110名学生的数学成绩，并作出了频数分布统计表如下：

     

    分组

    [70,80）

    [80,90）

    [90,100）

    [100,110）

    频数

    3

    4

    8

    15

    分组

    [110,120）

    [120,130）

    [130,140）

    [140,150]

    频数

    15

    x

    3

    2

        甲校：

     

     

    分组

    [70,80）

    [80,90）

    [90,100）

    [100,110）

    频数

    1

    2

    8

    9

    分组

    [110,120）

    [120,130）

    [130,140）

    [140,150]

    频数

    10

    10

    y

    3

        乙校：

     

     

     

    （Ⅰ）计算x，y的值。

    （Ⅱ）若规定考试成绩在[120,150]内为优秀，请分别估计两个学校数学成绩的优秀率。

     

     

    甲校

    乙校

    总计

    优秀

     

     

     

    非优秀

     

     

     

    总计

     

     

     

     

     

     

     

     

     

    （Ⅲ）由以上统计数据填写右面2×2列联表，并判断是否有90%的把握认为两个学校的数学成绩有差异。

    参考数据与公式：

    由列联表中数据计算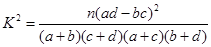

    临界值表

     

     

     

    查看答案和解析>>

    甲、乙两所学校高三年级分别有1200人，1000人，为了了解两所学校全体高三年级学生在该地区六校联考的数学成绩情况，采用分层抽样方法从两所学校一共抽取了110名学生的数学成绩，并作出了频数分布统计表如下：

    甲校：

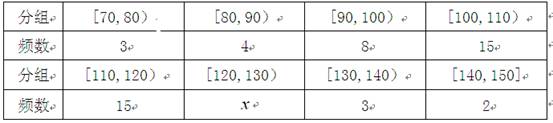
    乙校：

    (1)计算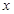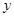，的值；

    (2)若规定考试成绩在[120,150]内为优秀，请分别估计两所学校数学成绩的优秀率；

    (3)由以上统计数据填写下面2×2列联表，并判断是否有90%的把握认为两所学校的数学成绩有差异.

     

    甲校

    乙校

    总计

    优秀

     

     

     

    非优秀

     

     

     

    总计

     

     

     

     

     

     

     

     

     

    参考数据与公式：

    由列联表中数据计算

    临界值表

    0.10

    0.05

    0.010

     

     

    查看答案和解析>>

    （08年安徽皖南八校联考）(本小题满分13分)

    袋中有红球和黄球若干个，从中任摸一球，摸得红球的概率为，摸得黄球的概率为．若从中任摸一球，放回再摸，第次摸得红球，则记＝1，摸得黄球，则记＝一1．令…．

    （1）当==时，记，求的分布列及数学期望；

    （2)当＝，＝时，求且（＝1，2，3，4）的概率．

     

    查看答案和解析>>

    甲乙两个学校高三年级分别有1200人，1000人，为了了解两个学校全体高三年级学生在该地区六校联考的数学成绩情况，采用分层抽样方法从两个学校一共抽取了110名学生的数学成绩，并作出了频数分布统计表如下：
    甲校：
    分组 [70，80） [80，90） [90，100） [100，110）
    频数 3 4 8 15
    分组 [110，120） [120，130） [130，140） [140，150]
    频数 15 x 3 2
    乙校：
    分组 [70，80） [80，90） [90，100） [100，110）
    频数 1 2 8 9
    分组 [110，120） [120，130） [130，140） [140，150]
    频数 10 10 y 3
    （Ⅰ）计算x，y的值．
    甲校 乙校 总计
    优秀
    非优秀
    总计
    （Ⅱ）若规定考试成绩在[120，150]内为优秀，请分别估计两个学校数学成绩的优秀率．
    （Ⅲ）由以上统计数据填写右面2×2列联表，并判断是否有90%的把握认为两个学校的数学成绩有差异．
    参考数据与公式：
    由列联表中数据计算K2=
    n(ad-bc)2
    (a+b)(c+d)(a+c)(b+d)

    临界值表
    P（K≥k0） 0.10 0.05 0.010
    k0 2.706 3.841 6.635

    查看答案和解析>>

    一、选择题：本大题共10小题，每小题5分，共50分．

    题号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    解答

    B

    D

    A

    B

    D

    B

    D

    C

    D

    C

    二、填空题：本大题共7小题，每小题4分，共28分

    11．        负                                   12．　　　　　　　    　　　

    13．                                  14．                         　      

    15．       2                                     16．      2125                  

    17．                              

    三、解答题：本大题共5小题，共72分．解答应写出文字说明，证明过程或演算步骤．

    18．解：（1）=，得：=，

    即：，      …………………………………………………………３分

      又∵０＜＜，

    ∴=．               …………………………………………………………５分

    （2）直线方程为：．

    ，点到直线的距离为：．

    ∵

    ∴，    …………………………………………………………9分

     ∴，  …………………………………………………………11分

    又∵０＜＜，       

     ∴sin＞0，cos＜0； …………………………………………………………12分

    ∴  

     ∴sin-cos=    ……………14分

    19.(Ⅰ)证明：连Ａ1B，Ｄ1C.

    ……２分　　

    连结，则

    又，故D1E⊥平面AB1F．     ………………………………………5分

    (Ⅱ)由(Ⅰ)知，Ｅ为棱BC的中点．

       ………………9分

    (Ⅲ).               ………………………11分

    在中，

     ………………………14分

    20. (Ⅰ)证明:令

    ，总有恒成立．

    ，总有恒成立．

    即

    令

    令

    故函数是奇函数.              ………………………………………………5分

    (Ⅱ) ，

    ．…………………………………………8分

    ……………………………………………………………………………10分

    (Ⅲ)

    ……………………………………………………………………………15分

    21．解：（Ⅰ）若为等腰直角

    三角形，所以有OA=OF2，即b=c ．  ………2分

    所以     …………５分

       （Ⅱ）由题知

    其中，．

    由　…８分

    将B点坐标代入，

    解得．　　①　　　　　……………………………………………………10分

    又由 ② …12分

    由①, ②解得,

    所以椭圆方程为．　　　 　……………………………………………14分

    22．解：  

    （Ⅰ）由题意，得

    所以，         …………………………………………5分

       （Ⅱ）由（Ⅰ）知，，

     

     

    －4

    （-4，-2）

    －2

    1

     

    +

    0

    －

    0

    +

     

     

    极大值

    极小值

     

    函数值

    －11

     

    13

     

     

    4

    在[－4，1]上的最大值为13，最小值为－11。     …………………10分

    （Ⅲ）

    或．所以存在或，使． ……………15分

     

     


    同步练习册答案