（本小题满分13分）．设全集U=R，集合，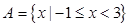 

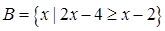
（1）求；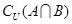

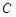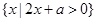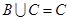（2）若集合=，满足，求实数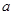的取值范围.

（本小题满分13分）

某市4997名学生参加高中数学会考，得分均在60分

以上，现从中随机抽取一个容量为500的样本，制成

如图a所示的频率分布直方图．

（Ⅰ）由频率分布直方图可知本次会考的数学平均分为

81分．请估计该市得分在区间的人数；

（Ⅱ）如图b所示茎叶图是某班男女各4名学生的得分情况，

现用简单随机抽样的方法，从这8名学生中，抽取男

女生各一人，求女生得分不低于男生得分的概率．

（本小题满分13分）．设全集U=R，集合，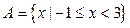 
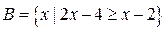
（1）求；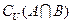
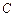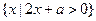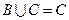（2）若集合=，满足，求实数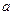的取值范围.

（本小题满分13分）

甲乙两队参加奥运知识竞赛，每队3人，每人回答一个问题，答对者为本队赢得一分，答错得零分.假设甲队中每人答对的概率均为，乙队中3人答对的概率分别为且各人正确与否相互之间没有影响.用ξ表示甲队的总得分.

（Ⅰ）求随机变量ξ分布列和数学期望；      

(Ⅱ)用A表示“甲、乙两个队总得分之和等于3”这一事件，用B表示“甲队总得分大于乙队总得分”这一事件，求P(AB).

（本小题满分13分）

甲乙两队参加奥运知识竞赛，每队3人，每人回答一个问题，答对者为本队赢得一分，答错得零分.假设甲队中每人答对的概率均为，乙队中3人答对的概率分别为且各人正确与否相互之间没有影响.用ξ表示甲队的总得分.

（Ⅰ）求随机变量ξ分布列和数学期望；      

(Ⅱ)用A表示“甲、乙两个队总得分之和等于3”这一事件，用B表示“甲队总得分大于乙队总得分”这一事件，求P(AB).