
题目列表(包括答案和解析)
一个同学在解决“已知在△ABC中,若sinA=![]() ,cosB=
,cosB=![]() ,求cosC的值”这一问题时给出了下面的解题步骤:
,求cosC的值”这一问题时给出了下面的解题步骤:
由于sinA=![]() ,则cosA=±
,则cosA=±![]() ,又cosB=
,又cosB=![]() ,则sinB=
,则sinB=![]() .
.
所以cosC=cos[π-(A+B)]=-cos(A+B)=sinAsinB-cosAcosB.
当cosA=![]() 时,cosC=
时,cosC=![]() ;当cosA=-
;当cosA=-![]() 时,cosC=
时,cosC=![]() .
.
综上可知cosC=![]() 或cosC=
或cosC=![]() .
.
这个同学的解题过程是否正确?
(1)当k=0时,若g(x)=![]() 的定义域为R,求实数m的取值范围;
的定义域为R,求实数m的取值范围;
(2)给出定理:若函数f(x)在[a,b]上连续,且f(a)·f(b)<0,则函数y=f(x)在区间(a,b)内有零点,即存在x0∈(a,b),使f(x0)=0.运用此定理,试判断当k>1时,函数f(x)在[k,2k]内是否存在零点.
(文)已知数列{an}的前n项和为Sn,a1=2,且nan+1=Sn+n(n+1)(n∈N*).
(1)求an;
(2)设bn=![]() ,求{bn}的最大项.
,求{bn}的最大项.
| π |
| 4 |
| fn(θ) | fn(θ)的 单调性 |
fn(θ)的最小值及取得最小值时θ的取值 | fn(θ)的最大值及取得最大值时θ的取值 |
| n=1 | |||
| n=2 | |||
| n=3 | |||
| n=4 | |||
| n=5 | |||
| n=6 |
| 1-x |
| 1+x |
| 1 |
| 2008 |
| 1 |
| 2008 |
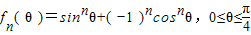 ,其中n为正整数.
,其中n为正整数.| fn(θ) | fn(θ)的 单调性 | fn(θ)的最小值及取得最小值时θ的取值 | fn(θ)的最大值及取得最大值时θ的取值 |
| n=1 | |||
| n=2 | |||
| n=3 | |||
| n=4 | |||
| n=5 | |||
| n=6 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com