
题目列表(包括答案和解析)
(本题满分12分)
如下图,某地有三家工厂,分别位于矩形ABCD 的顶点A、B 及CD的中点P 处,已知AB=20km,CB =10km ,为了处理三家工厂的污水,现要在矩形ABCD 的区域上(含边界),且与A、B等距离的一点O处建造一个污水处理厂,并铺设排污管道AO、BO、OP ,设排污管道的总长度为 km.
km.
(1)按下列要求写出函数关系式:
①设∠BAO=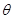 (rad),将
(rad),将 表示成
表示成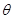 的函数;
的函数;
②设OP (km) ,将
(km) ,将 表示成
表示成 的函数.
的函数.
(2)请选用(1)中的一个函数关系式,确定污水处理厂的位置,使铺设的排污管道总长度最短.
(本题满分12分) (I)对于计算![]() 值的一个算法,其算法步骤如下:
值的一个算法,其算法步骤如下:
第一步,令![]()
第二步,若 (1) 成立,则执行第三步;否则,输出![]() ,并结束算法 。
,并结束算法 。
第三步,计算![]()
第四步,计算![]() ,返回第二步。
,返回第二步。
在算法步骤中 (1) 处填上合适的条件,使之能完成该题算法功能(请写在答题卷上);
(II)画出输入一个正整数![]() ,求
,求![]() 值的程序框图。
值的程序框图。
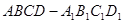 中,
中,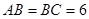 ,用过
,用过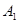 ,
,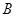 ,
,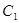 三点的平面截去长方体的一个角后,留下如图的几何体,且这几何体的体积为120.
三点的平面截去长方体的一个角后,留下如图的几何体,且这几何体的体积为120.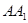 的长;
的长;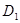 到平面
到平面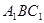 的距离.
的距离.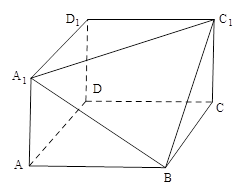
(本题满分12分)
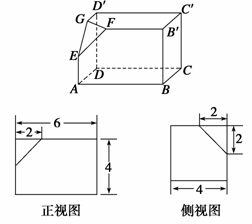
如下的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位: )
)
(Ⅰ)在正视图下面,按照画三视图的要求画出该多面体的俯视图;
(Ⅱ)按照给出的尺寸,求该多面体的体积;
(Ⅲ)在所给直观图中连结 ,证明:
,证明: ∥面
∥面

(本题满分12分)
如下的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:![]() )
)
(Ⅰ)在正视图下面,按照画三视图的要求画出该多面体的俯视图;
(Ⅱ)按照给出的尺寸,求该多面体的体积;
(Ⅲ)在所给直观图中连结![]() ,证明:
,证明:![]() ∥面
∥面![]()
一、选择题
1.D. 2.A. 3.B. 4.C. 5.B. 6.A.
7.C. 8.D. 9.D. 10.C. 11.B. 12.B.
二、填空题:
13.%20数学文科.files/image161.gif) .
14.5. 15.
.
14.5. 15.%20数学文科.files/image163.gif) 或
或%20数学文科.files/image165.gif) . 16.②.
. 16.②.
三、解答题:本大题共6小题,共74分.解答应写出文字说明.证明过程或演算步骤.
17.本题主要考查两角和与差的三角函数公式、二倍角公式,三角函数的图象与性质等基础知识;考查运算求解能力.满分12分.
%20数学文科.files/image167.gif)
%20数学文科.files/image169.gif)
%20数学文科.files/image171.gif) .
.
%20数学文科.files/image173.gif) ,
,
%20数学文科.files/image175.gif) ,
,
即%20数学文科.files/image177.gif) 时,f(x)单调递增.
时,f(x)单调递增.
∴f(x)的单调递增区间为[%20数学文科.files/image179.gif) ,
,%20数学文科.files/image181.gif) ]
]%20数学文科.files/image183.gif) .
.
18.(1)记“编号的和为%20数学文科.files/image185.gif) ”的事件
”的事件%20数学文科.files/image187.gif) ,事件
,事件%20数学文科.files/image187.gif) 所包含的基本事件为
所包含的基本事件为%20数学文科.files/image190.gif) 、
、%20数学文科.files/image192.gif) 、
、%20数学文科.files/image194.gif) 、
、%20数学文科.files/image196.gif) 、
、%20数学文科.files/image198.gif) ,共5个, ∴
,共5个, ∴%20数学文科.files/image200.gif)
(2)记“甲赢”为事件%20数学文科.files/image202.gif) ,事件
,事件%20数学文科.files/image202.gif) 所包含的基本事件为
所包含的基本事件为%20数学文科.files/image205.gif) 、
、%20数学文科.files/image207.gif) 、
、%20数学文科.files/image190.gif) 、
、%20数学文科.files/image210.gif) 、
、%20数学文科.files/image192.gif) 、
、%20数学文科.files/image213.gif) 、
、%20数学文科.files/image194.gif) 、
、%20数学文科.files/image216.gif) 、
、%20数学文科.files/image196.gif) 、
、%20数学文科.files/image219.gif) 、
、%20数学文科.files/image198.gif) 、
、%20数学文科.files/image222.gif) 、
、%20数学文科.files/image224.gif) ,共13个, ∴
,共13个, ∴%20数学文科.files/image226.gif) ,
,
19.本题主要考查空间几何体的直观图、三视图,空间线面的位置关系等基础知识;考查空间想像能力及推理论证能力.满分12分.
(Ⅰ)如图
%20数学文科.files/image228.jpg)
俯视图
(Ⅱ)所求多面体的体积
%20数学文科.files/image230.gif) .
.
(Ⅲ)证明:如图,在长方体%20数学文科.files/image232.gif) 中,连接
中,连接%20数学文科.files/image234.gif) ,则
,则%20数学文科.files/image234.gif) ∥
∥%20数学文科.files/image237.gif) .
.
%20数学文科.files/image239.jpg)
因为E,G分别为%20数学文科.files/image241.gif) 的中点,
的中点,
所以%20数学文科.files/image234.gif) ∥
∥%20数学文科.files/image243.gif) ,从而
,从而%20数学文科.files/image243.gif) ∥
∥%20数学文科.files/image237.gif) .
.
又%20数学文科.files/image246.gif) ,所以
,所以%20数学文科.files/image237.gif) ∥平面EFG.
∥平面EFG.
20. 本题主要考查等差数列、数列求和等基础知识;考查推理论证与运算求解能力;考查化归与转化思想.满分12分.
(Ⅰ)设数列{an}的公差为d,则
%20数学文科.files/image249.gif)
解得%20数学文科.files/image251.gif) .
.
因此,an=-1+2(n-1)=2n-3.
(Ⅱ)由已知%20数学文科.files/image143.gif) (1)得,
(1)得,
当n≥2时,%20数学文科.files/image253.gif) (2).
(2).
由(1)-(2)得%20数学文科.files/image255.gif) ,
,
所以%20数学文科.files/image257.gif) ,又
,又%20数学文科.files/image259.gif) ,
,
故%20数学文科.files/image261.gif) .
.
在式(1)中,令n=1得,%20数学文科.files/image263.gif) ,
,
又%20数学文科.files/image265.gif) ,故
,故%20数学文科.files/image267.gif) .
.
所以%20数学文科.files/image269.gif) .
.
21.本题主要考查直线与椭圆的位置关系等基础知识;考查运算求解能力及化归与转化思想.满分12分.
(Ⅰ)由题设b=%20数学文科.files/image149.gif) ,c=2,从而a2=b2+c2=6,
,c=2,从而a2=b2+c2=6,
所以椭圆C的方程为%20数学文科.files/image271.gif) .
.
(Ⅱ)假设斜率为k的直线l与椭圆C交于A、B两点,使得∠AOB为锐角,
设直线l的方程为y=k(x - 2).
%20数学文科.files/image273.jpg)
%20数学文科.files/image275.jpg)
%20数学文科.files/image277.jpg)
所以满足题意的的直线l存在,斜率k的取值范围为%20数学文科.files/image279.gif)
方法二:
同方法一得到%20数学文科.files/image281.gif) .
.
%20数学文科.files/image283.jpg)
所以满足题意的的直线l存在,斜率k的取值范围为%20数学文科.files/image279.gif)
22.本题主要考查利用导数研究函数的性质,考查运算求解能力及数形结合思想.满分14分.
(Ⅰ)%20数学文科.files/image285.gif) ,由
,由%20数学文科.files/image287.gif) 得,
得,
%20数学文科.files/image289.gif) ,解得
,解得%20数学文科.files/image291.gif) .
.
(Ⅱ)由(Ⅰ)知,
%20数学文科.files/image293.gif) ,
,
%20数学文科.files/image295.gif) .
.
当%20数学文科.files/image297.gif) 时,
时,%20数学文科.files/image299.gif) ;
;
当%20数学文科.files/image301.gif) 时,
时,%20数学文科.files/image303.gif) ;
;
%20数学文科.files/image305.gif) 时,
时,%20数学文科.files/image299.gif) .
.
所以%20数学文科.files/image154.gif) 的单调增区间是
的单调增区间是%20数学文科.files/image308.gif) ;
;%20数学文科.files/image154.gif) 的单调减区间是
的单调减区间是%20数学文科.files/image310.gif) .
.
(Ⅲ)由(Ⅱ)知,%20数学文科.files/image154.gif) 在
在%20数学文科.files/image312.gif) 内单调递增,在
内单调递增,在%20数学文科.files/image310.gif) 内单调递减,在
内单调递减,在%20数学文科.files/image315.gif) 上单调递增,且当
上单调递增,且当%20数学文科.files/image317.gif) 或
或%20数学文科.files/image319.gif) 时,
时,%20数学文科.files/image321.gif) .
.
所以%20数学文科.files/image154.gif) 的极大值为
的极大值为%20数学文科.files/image323.gif) ,极小值为
,极小值为%20数学文科.files/image325.gif) .
.
又因为%20数学文科.files/image327.gif) ,
,
%20数学文科.files/image329.gif) .
.
当且仅当%20数学文科.files/image331.gif) ,直线
,直线%20数学文科.files/image156.gif) 与
与%20数学文科.files/image334.gif) 的图象有三个交点.
的图象有三个交点.
所以,%20数学文科.files/image082.gif) 的取值范围为
的取值范围为%20数学文科.files/image336.gif) .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com