
题目列表(包括答案和解析)
某宾馆有相同标准的床位100张,根据经验,当该宾馆的床价(即每张床每天的租金)不超过10元时,床位可以全部租出,当床位高于10元时,每提高1元,将有3张床位空闲.为了获得较好的效益,该宾馆要给床位一个合适的价格,条件是:①要方便结帐,床价应为1元的整数倍;② 该宾馆每日的费用支出为575元,床位出租的收入必须高于支出,而且高出得越多越好.若用![]() 表示床价,用
表示床价,用![]() 表示该宾馆一天出租床位的净收入(即除去每日的费用支出后的收入)
表示该宾馆一天出租床位的净收入(即除去每日的费用支出后的收入)
(1)把![]() 表示成
表示成![]() 的函数,并求出其定义域;
的函数,并求出其定义域;
(2)试确定该宾馆将床位定价为多少时既符合上面的两个条件,又能使净收入最多?
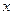 表示床价,用
表示床价,用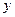 表示该宾馆一天出租床位的净收入(即除去每日的费用支出后的收入)
表示该宾馆一天出租床位的净收入(即除去每日的费用支出后的收入)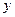 表示成
表示成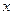 的函数,并求出其定义域;
的函数,并求出其定义域;如图所示,四面体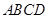 被一平面所截,截面
被一平面所截,截面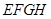 是一个平行四边形.求证:
是一个平行四边形.求证: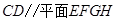 ;
;
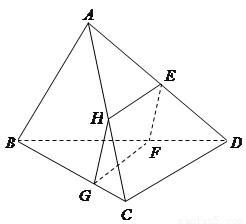
【答案】(理)证明: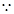 EH∥FG,EH
EH∥FG,EH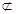 面
面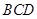 ,
,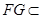 面
面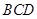
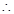 EH∥面
EH∥面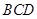 ,又
,又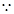 CD
CD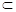 面
面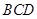 ,
,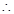 EH∥CD, 又EH
EH∥CD, 又EH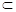 面EFGH,CD
面EFGH,CD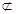 面EFGH
面EFGH
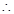 EH∥BD
EH∥BD
【解析】本试题主要是考查了空间四面体中线面位置关系的判定。
要证明线面平行可知通过线线平行,结合判定定理得到结论。
有时可用函数f(x)= 描述学习某学科知识的掌握程度,其中x表示某学科知识的学习次数(x∈N+),f(x)表示对该学科知识的掌握程度,正实数a与学科知识有关.
描述学习某学科知识的掌握程度,其中x表示某学科知识的学习次数(x∈N+),f(x)表示对该学科知识的掌握程度,正实数a与学科知识有关.
(1)证明:当x≥7时,掌握程度的增加量f(x+1)-f(x)总是下降;
(2)根据经验,学科甲、乙、丙对应的a的取值区间分别为(115,121],(121,127],(127,133].当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.
分析:根据已知条件作差,结合综合法可以确定作差所得的函数为减函数,从而得出结论;又根据函数模型代入数据可以解得参数a的近似值,通过对近似值所在区间加以判断并选择相应的学科.
某宾馆有相同标准的床位
l00张,根据经验,当该宾馆的床价(即每张床每天的租金)不超过10元时,床位可以全部租出;当床位价格高于10元时,每提高1元,将有3张床位空闲.为了获得较好的效益,该宾馆要给床位定一个合适的价格,条件是:①要方便结帐,床价应为1元的整数倍;②该宾馆每日的费用支出为575元,床位出租的收入必须高于支出,而且高出得越多越好,若用x表示床价,用y表示该宾馆一天出租床位的净收入(即除去每日的费用支出后的收入).(1)
把y表示成x的函数;(2)
试确定,该宾馆将床价定为多少元时,即符合上面的两个条件又能使净收入最多?湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com