
题目列表(包括答案和解析)
| 销售单价x(元) | 30 | 40 | 45 | 50 |
| 日销售量y(件) | 60 | 30 | 15 | 0 |
 某商场一批进价30元/件的商品,在市场试销中发现,此商品的销售单价x元,与件数y(件)之间有如下关系:
某商场一批进价30元/件的商品,在市场试销中发现,此商品的销售单价x元,与件数y(件)之间有如下关系:| x | … | 30 | 40 | 45 | 50 | … |
| y | … | 60 | 40 | 15 | 0 | … |
(14分)某商场经营一批进价是每件30元的商品,在市场销售中发现此商品的销售单
价 元与日销售量
元与日销售量 件之间有如下关系:
件之间有如下关系:
|
销售单价 |
30 |
40 |
45 |
50 |
|
日销售量 |
60 |
30 |
15 |
0 |
(1)
在所给坐标系中,根据表中提供的数据描出实数对 对应的点,并确定
对应的点,并确定 与
与 的一个函数关系式
的一个函数关系式 ;www.zxxk.com
;www.zxxk.com
(2)设经营此商品的日销售利润为 元,根据上述关系式写出
元,根据上述关系式写出 关于
关于 的函数关系式,并指出销售单价
的函数关系式,并指出销售单价 为多少时,才能获得最大日销售利润。
为多少时,才能获得最大日销售利润。
| 销售单价x(元) | 30 | 40 | 45 | 50 |
| 日销售量y(件) | 60 | 30 | 15 |
已知 ,(其中
,(其中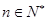 )
)
⑴求 及
及 ;
;
⑵试比较 与
与 的大小,并说明理由.
的大小,并说明理由.
【解析】第一问中取 ,则
,则 ;
…………1分
;
…………1分
对等式两边求导,得
取 ,则
,则 得到结论
得到结论
第二问中,要比较 与
与 的大小,即比较:
的大小,即比较: 与
与 的大小,归纳猜想可得结论当
的大小,归纳猜想可得结论当 时,
时, ;
;
当 时,
时, ;
;
当 时,
时, ;
;
猜想:当 时,
时, 运用数学归纳法证明即可。
运用数学归纳法证明即可。
解:⑴取 ,则
,则 ;
…………1分
;
…………1分
对等式两边求导,得 ,
,
取 ,则
,则 。 …………4分
。 …………4分
⑵要比较 与
与 的大小,即比较:
的大小,即比较: 与
与 的大小,
的大小,
当 时,
时, ;
;
当 时,
时, ;
;
当 时,
时, ;
…………6分
;
…………6分
猜想:当 时,
时, ,下面用数学归纳法证明:
,下面用数学归纳法证明:
由上述过程可知, 时结论成立,
时结论成立,
假设当 时结论成立,即
时结论成立,即 ,
,
当 时,
时,
而
∴
即 时结论也成立,
时结论也成立,
∴当 时,
时, 成立。
…………11分
成立。
…………11分
综上得,当 时,
时, ;
;
当 时,
时, ;
;
当 时,
时,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com