
题目列表(包括答案和解析)
(14分)在![]()
![]()
![]()
![]() 。
。
![]() (Ⅰ)指出点
(Ⅰ)指出点![]() 所在的位置,并给予证明;
所在的位置,并给予证明;
![]() (Ⅱ)设
(Ⅱ)设![]() 求函数
求函数![]() 的最小值g(x),并求出相应的
的最小值g(x),并求出相应的![]() 值;
值;
在平面直角坐标系中,已知三个点列![]() ,其中
,其中![]()
![]() ,满足向量
,满足向量![]() 与向量
与向量![]() 共线,且点列
共线,且点列![]() 在方向向量为
在方向向量为![]() 的直线上,
的直线上,![]() 。
。
(1) 试用![]() 与
与![]() 表示
表示![]() ;
;
(2) 若![]() 与
与![]() 两项中至少有一项是
两项中至少有一项是![]() 的最小值,试求
的最小值,试求![]() 的取值范围。
的取值范围。
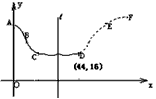
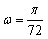 。
。
 ,
, 
 。
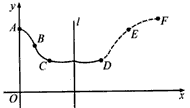
。
一、选择题:本大题共有8个小题,每小题5分,共40分;在每个小题给出的四个选项中有且仅有一个是符合题目要求的。
1―8 BDABADBC
二、填空题:本大题共有6个小题,每小题5分,共30分;请把答案写在相应的位置上。
9.5 10. 11.7 12.
11.7 12. 13.
13. 14.
14.
三、解答题:本大题共6个小题,共80分;解答应写出文字说明,证明过程或演算步骤。
15.(本题满分13分)
解:(1)

(2)

16.(本题满分13分)
解: 用A,B,C分别表示事件甲、乙、丙面试合格.
由题意知A,B,C相互独立,且
P(A)=P(B)=P(C)= .
.
(Ⅰ)至少有1人面试合格的概率是
 …………………6分
…………………6分
(2)没有人签约的概率为

 ………………13分
………………13分
17.(本题满分13分)
解法1:(1)连结A1B,则D1E在侧面ABB
又∵A1B⊥AB1,
|